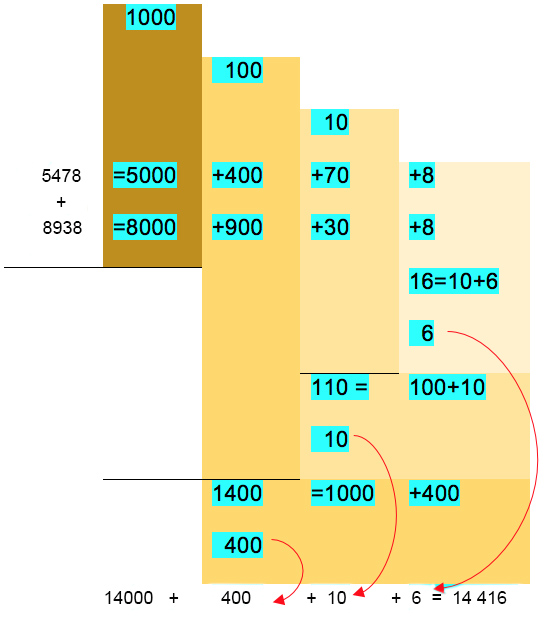
La notación desarrollada ayuda a entender razonadamente el algoritmo de la suma, evitando aprenderlo de forma mecánica pues confirma que sólo se pueden sumar las unidades con las unidades, decenas con decenas, centenas con centenas, etc., es decir, dígitos en la misma posición en las cantidades a sumar. El proceso se inicia con las unidades.

Los ejemplos siguientes lo ratificarán. Efectuaremos las sumas utilizando notación desarrollada empezando con las unidades.

Ejemplos:

• Suma 235 y 452

• Suma 4562 y 3312

¿Por qué al sumar se utilizan procesos de "llevar"? ¿Esto qué significa? Analiza el ejemplo que sigue, al sumar verticalmente 59 y 96, decimos $9 + 6 = 15$, escribimos 5 y llevamos uno. ¿Qué significa llevar uno?

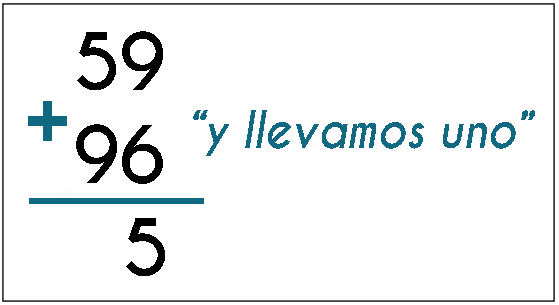
Como ya se mostró y como se muestra en los ejemplos siguientes, debemos sumar unidades con unidades, decenas con decenas, centenas con centenas, etc. Si al estar haciendo esto nos queda en la columna de las unidades un resultado con decenas, o en la columna de las decenas un resultado con centenas, se escribe el número en notación desarrollada y se acomoda cada dígito en su lugar. Por ejemplo $9 + 6$ da $15$. El $15$ se descompone en $10 + 5$, se escribe el 5 en las unidades y se dice que se lleva 1 porque efectivamente se lleva una decena, que se escribe con un “1” en la columna de las decenas. Después, debemos sumar todos los elementos de la misma naturaleza (unidades con unidades, decenas con decenas, etc.), y finalmente dar el resultado en forma condensada.

Analiza los siguientes ejercicios:

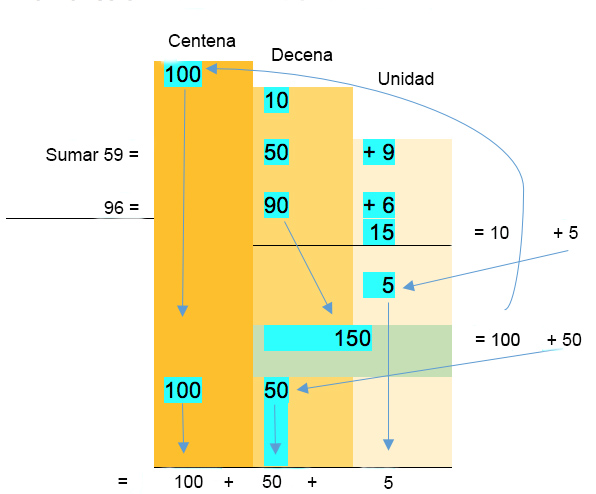
Podemos escribir solo una cifra, porque las unidades sólo pueden sumarse con las unidades, las decenas con las decenas, las centenas con las centenas, etc. (números de misma naturaleza). Por tanto, escribimos 5 unidades y decimos que llevamos una, porque efectivamente llevamos una decena. Para que se vea bien la decena utilizamos la notación desarrollada. Ya que se entienda bien el algoritmo podemos hacer la suma con la forma condensada.

Sumar 5478 con 8938

Podemos escribir sólo una cifra, porque las unidades solo pueden sumarse con las unidades, las decenas con las decenas, las centenas con las centenas, etc., (números de la misma naturaleza). Por tanto, escribimos 6 unidades y decimos que llevamos una, (una decena). $10 \, + \, 70 \, + \, 30 \, = \, 110 \, = \, 100 \, + \, 10 \, = \, 1 \,\, centena \, + \, 1 \,\, decena, \, etc.$

Toma lápiz y papel y resuelve los mismos ejercicios antes revisados con notación desarrollada, hasta que los entiendas bien. Compara tu procedimiento con el presentado aquí (que sabemos es larguísimo), el cual expusimos para que tengas idea del por qué “se llevan” números al sumar verticalmente.

Algoritmo de la adición usando notación condensada

Hacer todo lo anterior cada vez que sumamos sería muy tardado. Vamos a usar la forma más práctica, la notación condensada. El procedimiento es el mismo: se suman cifras de la misma naturaleza, es decir, unidades con unidades, decenas con decenas, etc., empezando con las unidades.

Toma lápiz y papel, realiza las siguientes sumas con notación condensada, y compara tu resultado con el aquí mostrado. Recuerda que se suman unidades con unidades, decenas con decenas, etc. Se inicia con las unidades.

Autoevaluación

Para el inicio a clases se entrega a los padres de familia la lista de útiles que tendrán que comprar, en la que aparece el nombre del artículo, su precio y el total que se gastará. La lista se presenta a continuación. Escribe las cantidades que faltan en los espacios que se encuentran vacíos.