Se denomina industria de la transformación de un país al conjunto de industrias que se dedican a convertir las materias primas o materiales (insumos) en productos que satisfagan las diversas necesidades de una sociedad (bienes de consumo). El proceso consiste en transformar estos insumos o entradas mediante procesos diversos con objeto de obtener los bienes de consumo o productos.

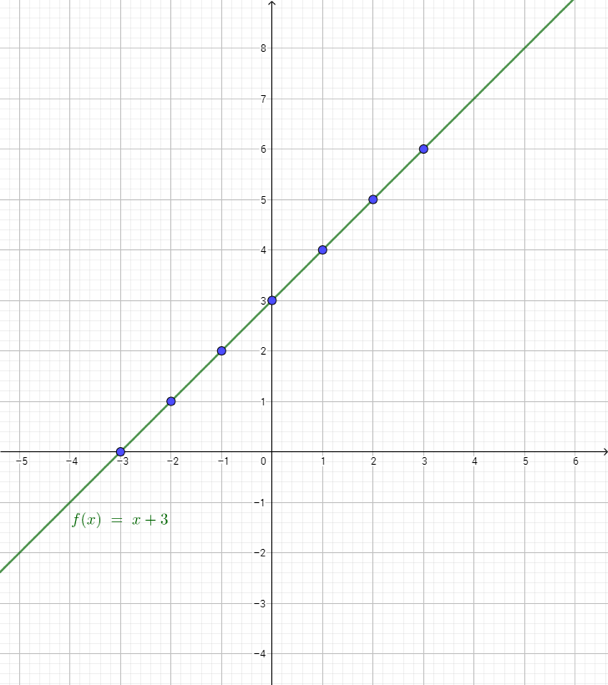
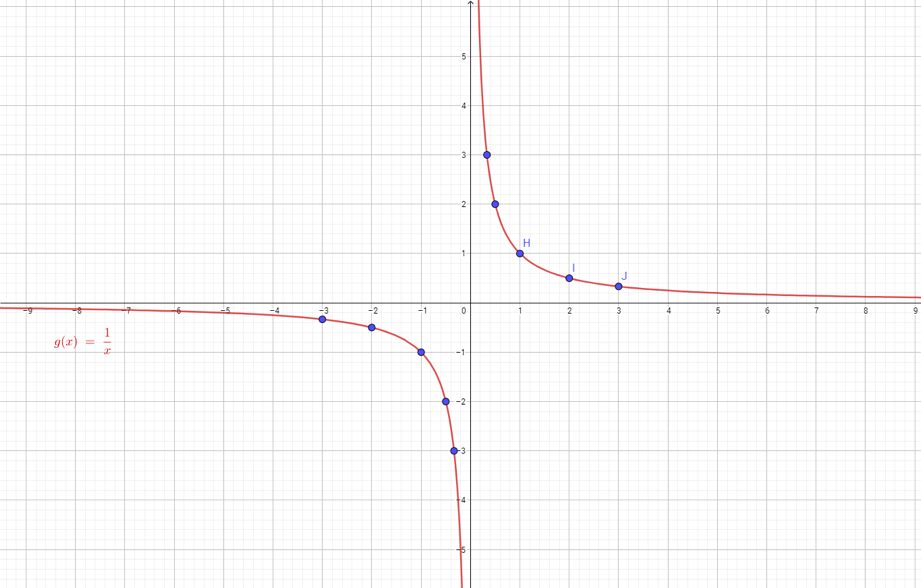
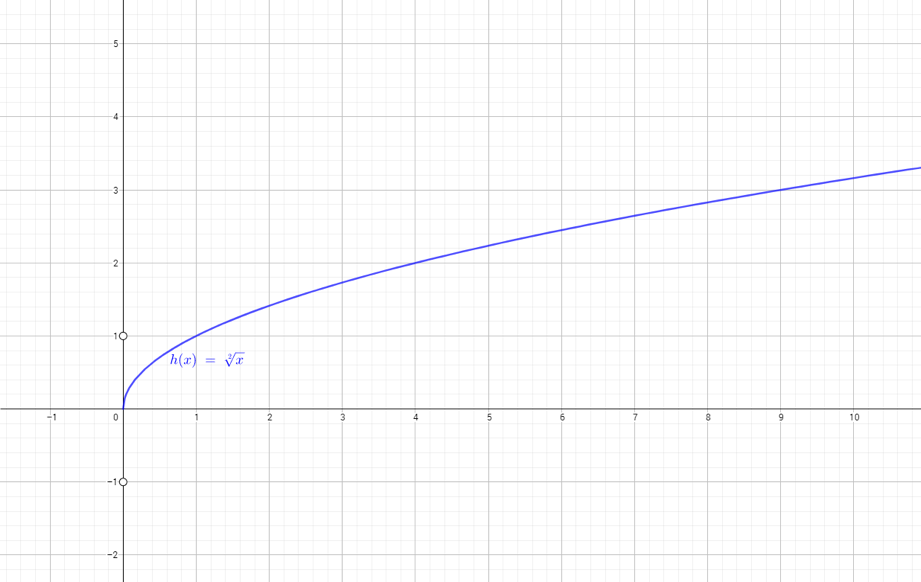
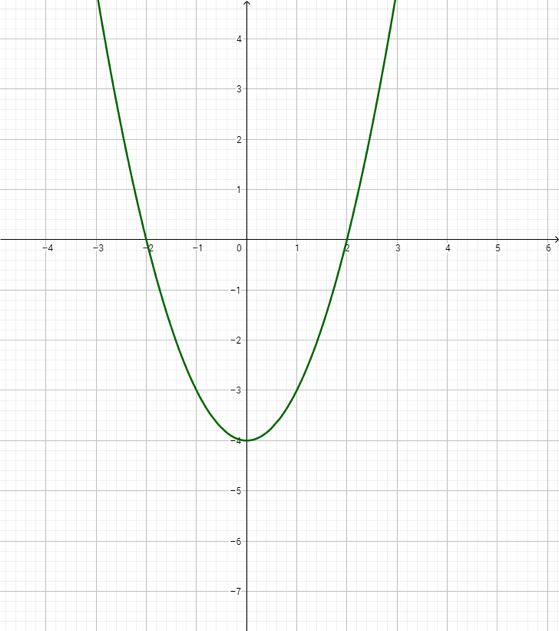
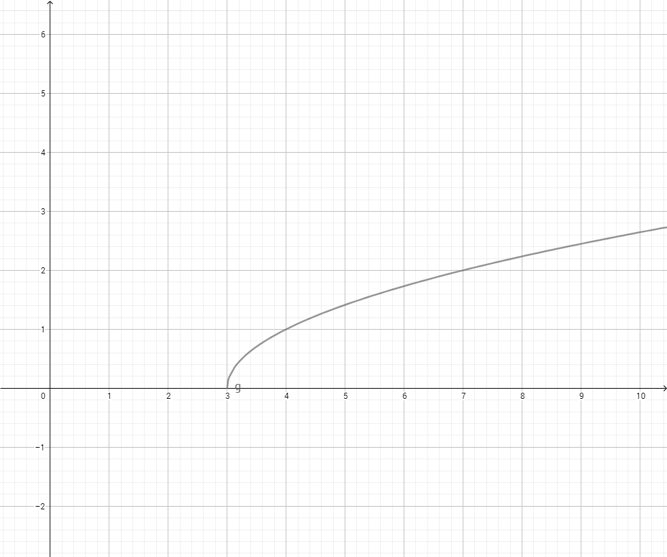
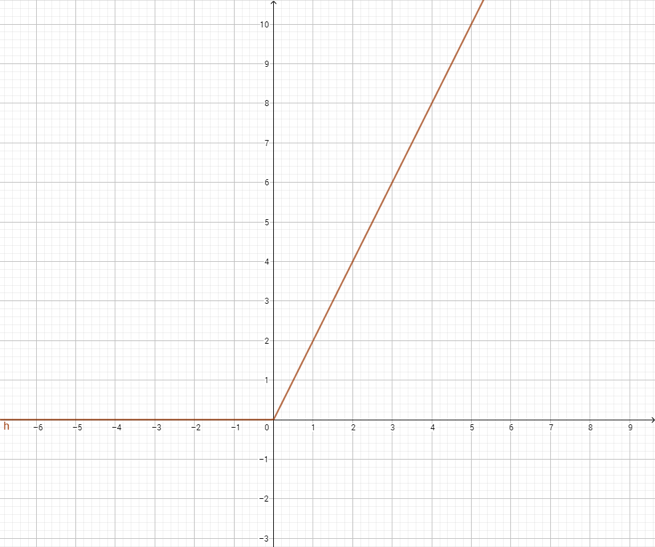
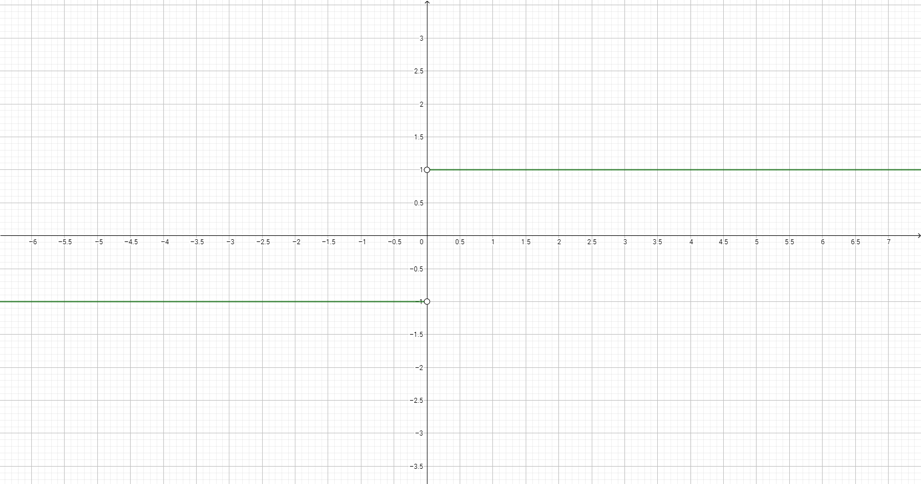
Aunque parezca ajeno, fíjate que las funciones en matemáticas trabajan de la misma manera:

1. Los valores de la variable independiente equivalen a los insumos o entradas de la función (a veces también se les llama argumentos).

2. La regla de correspondencia equivale al proceso de transformación.

3. Los valores de la variable dependiente equivalen a los bienes de consumo o salidas de la función, también conocidos como imágenes.

Dominio y Codominio de una función

En estos términos, decimos entonces que el dominio es el conjunto de valores de entrada, el rango (o imagen) es el conjunto de valores de salida de una función y el codominio es el conjunto que contiene al rango.

Veamos unos ejemplos:

• Considera la función $f(x)=x+3$. Esta función no tiene ninguna restricción en su dominio, es decir, la regla de correspondencia que la define, es aplicable a cualquier número real, por lo tanto su dominio es el conjunto de todos los números reales: $\mathbb{R}$. Si la función se llama $f$, el dominio se denota como $Dom_f$ y el codominio como $Cod_f$.

  Observa que su codominio también son todos los números reales pues si $x$ es un número real, $x+3$ también lo es. Entonces, escribimos que: $$Dom_f=\mathbb{R}=Cod_f$$

  Y solemos denotarla así: $$f: \mathbb{R} \to \mathbb{R}$$

• ¿Cómo obtenemos el rango de $f$? Dijimos que el rango de $f$ es el conjunto formado por todos los valores de “salida” de la función, es decir: $$Ran_f=\{y\in \mathbb{R}|y=f(x) \text{ para alguna } x \in \mathbb{R}\}$$

  Quiere decir que en el conjunto $Ran_f$ (a veces también denotado como $Im_f$) están todas las posible soluciones de la ecuación $$y=x+3$$ observa que para cada número real $x$ tenemos un número real $y$ por lo que todo número real es una posible solución, es decir, $Ran_f= \mathbb{R}$. Así, la imagen de $f$ -o su rango- son también todos los números reales.

• Ahora considera la función $g(x)=\frac{1}{x}$. Observa que esta función tiene una clara restricción en su dominio, como no es posible dividir por cero, entonces $0$ no pertenece a su dominio. Con los demás números reales no hay ningún problema, por lo que $Dom_g =\mathbb{R}-\{0\}$. En este caso también se tiene que $Cod_g=\mathbb{R}$.

  ¿Cuál sería el rango de $g$? por definición tenemos que es el conjunto $Ran_g= \{y \in \mathbb{R}| y=\frac{1}{x}\text{ para alguna } x \in \mathbb{R}\}$

  En la ecuación $y=\frac{1}{x}$ se tiene que $x$ sería solución, si y solamente si $x=\frac{1}{y}$ (sustituye este valor en la ecuación para comprobarlo).

  Por lo que el rango de $g$ será el conjunto $Ran_g= \{\frac{1}{y} |y \in \mathbb{R}\}$ y, como habíamos observado con el dominio de $g$ la expresión $\frac{1}{y}$ solamente tiene restricción para $y=0$ por lo que $Ran_g =\mathbb{R}-\{0\}$.

• Obtengamos ahora dominio, codominio y rango de la función $h(x)=\sqrt{x}$. Aquí también hay restricciones evidentes en el dominio pues la raíz cuadrada de números negativos no está definida. Entonces el dominio de $h$ está formado por los números reales no negativos, es decir, $$Dom_h=\{x \in \mathbb{R}| x\geq 0 \}$$ en notación de intervalos este conjunto se denota como $Dom_h=[0, \infty)$.

  El codominio serían los números reales pues la raíz cuadrada de un número real es nuevamente un número real, $Cod_h=\mathbb{R}$, sin embargo, notemos que todas las imágenes son no negativas por lo que $Ran_h=[0,\infty)$.

Gráfica de una función

Una herramienta muy útil para estudiar funciones es su gráfica, si $f$ es una función con dominio $A$, la gráfica de $f$ es el conjunto de pares ordenados $$\{(x,f(x)) \in \mathbb{R}^2|x\in A\}$$ es decir, el conjunto de puntos $(x,y)$ del plano, tales que $y=f(x)$. Observa que esta última expresión establece que la gráfica de una función también puede expresarse como una ecuación.

Conocer la gráfica de una función permite conocer su imagen y su comportamiento lo cual puede ser muy útil al estudiar un fenómeno modelado por tal función. Una forma de obtener la gráfica de una función es tabular algunos puntos y luego unirlos. Obtengamos por ejemplo, las gráficas de las funciones que vimos en los ejemplos anteriores:

1. $f(x)=x+3$

2. $g(x)=\frac{1}{x}$

Otra forma más sencilla es usar algún paquete de geometría dinámica como Geogebra.

3. $h(x)=\sqrt{x}$

Autoevaluación

Determina dominio y codominio de las funciones siguientes. Después obtén su rango y su gráfica.

1. $f(x)=x^{2}-4$

$Dom_f=\mathbb{R}$ $Cod_f=\mathbb{R}$ $Ran_f=[-4,\infty)$

2. $g(x)=\sqrt{x-3}$

$Dom_g=[3,\infty)$ $Cod_g=\mathbb{R}$ $Ran_g=[0,\infty)$

3. $h(x)=|x|+x$

$Dom_h=\mathbb{R}$ $Cod_h=\mathbb{R}$ $Ran_h=[0,\infty)$

4. $j(x)=\frac{x}{|x|}$

$Dom_j=\mathbb{R}-\{0\}$ $Cod_j=\mathbb{R}$ $Ran_j=\{1,-1\}$