Introducción
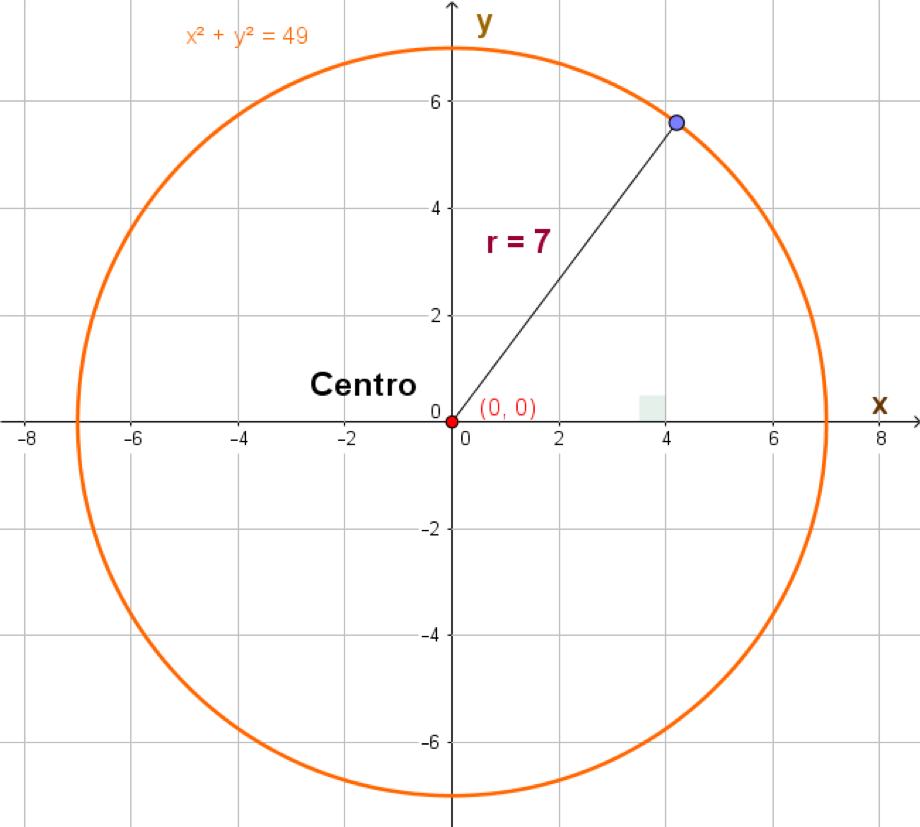
La circunferencia es el lugar geométrico de los puntos equidistantes a un punto fijo llamado centro. Es decir, todos los puntos de la circunferencia están a la misma distancia de su centro. Esta distancia, llamada radio de la circunferencia, se denota por la letra $r$ en la siguiente gráfica: se trata de una circunferencia de radio $r$ con centro en el origen -el punto de coordenadas $(0,0)$- del plano cartesiano.
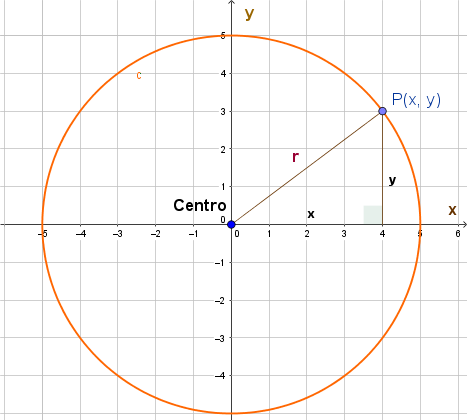
Observa el triángulo formado por los puntos $(0,0), (x,0)$ y $P(x,y)$. Se trata de un triángulo rectángulo. Su hipotenusa mide $r,$ su cateto horizontal mide $x$ y el cateto vertical mide $y.$ Sabemos que satisface el Teorema de Pitágoras, entonces $$x^2 + y^2 = r^2$$
Esta es la ecuación ordinaria de una circunferencia, de centro en el origen y radio $r> 0.$
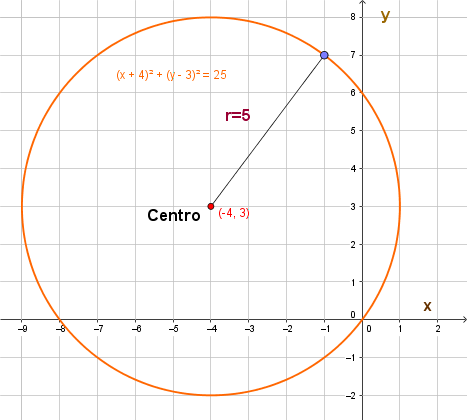
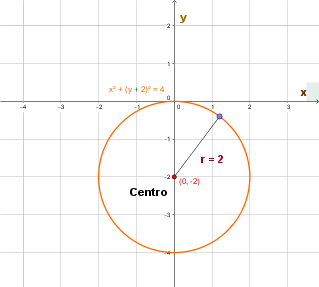
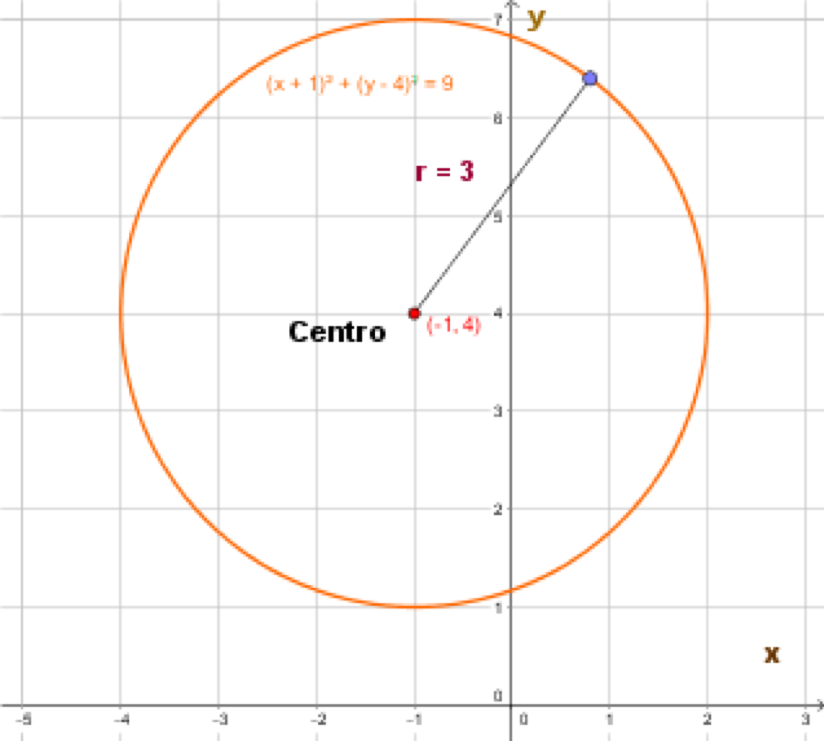
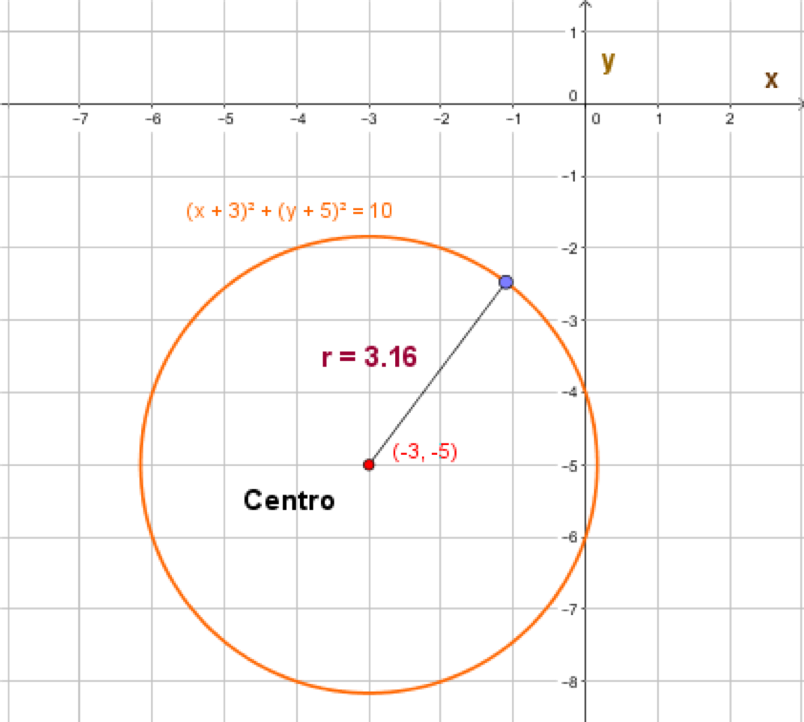
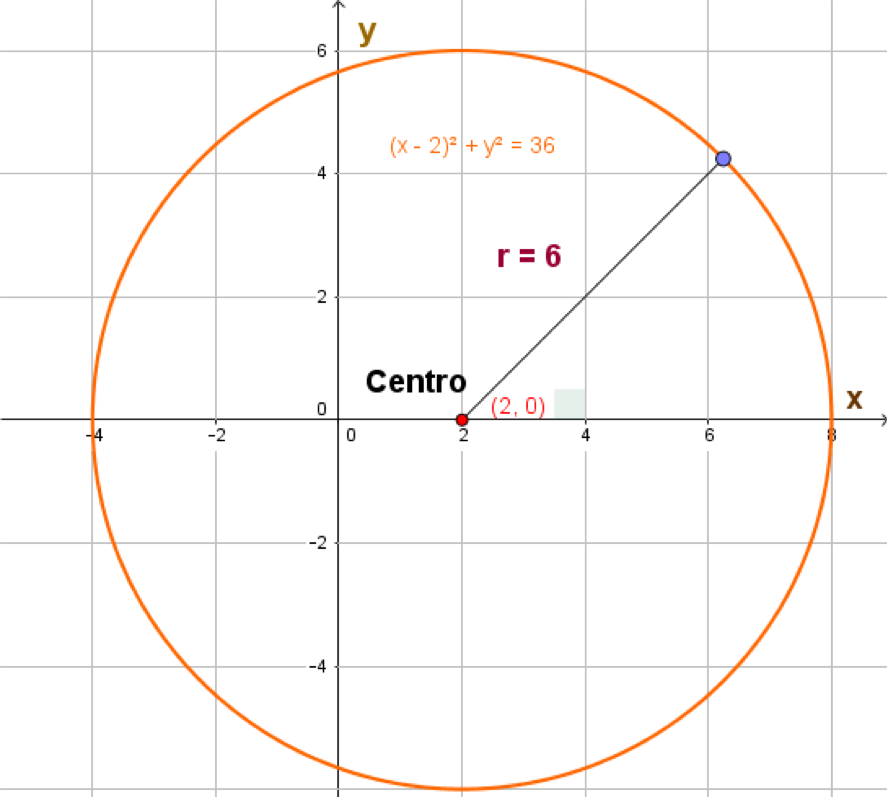
Si el centro de la circunferencia no coincide con el origen del plano, digamos que el centro es el punto $C(h,k),$ la ecuación toma la siguiente forma: $(x-h)^2 + (y-k)^2 = r^2.$ Nuevamente, aquí $r$ es el radio de la circunferencia.
Existe otra forma de representar la ecuación de una circunferencia de centro $C(h,k)$ y radio $r.$ Esta se obtiene desarrollando los binomios en la ecuación ordinaria:
$$(x-h)^2 + (y-k)^2 = r^2$$
$$ \Leftrightarrow x^2 - 2h + h^2 + y^2 - 2k + k^2 = r^2 $$
$$ \Leftrightarrow x^2 - 2h + h^2 + y^2 - 2k + k^2 - r^2 = 0 $$
Para simplificar esta expresión, se introducen las siguientes literales:
Sean $ D = -2h, E = -2k, F = h^2 + k^2 - r^2.$ Entonces, la ecuación queda como:
$x^2 + y^2 + Dx + Ey + F = 0$
Que se conoce como forma general de la ecuación de una circunferencia.