Introducción

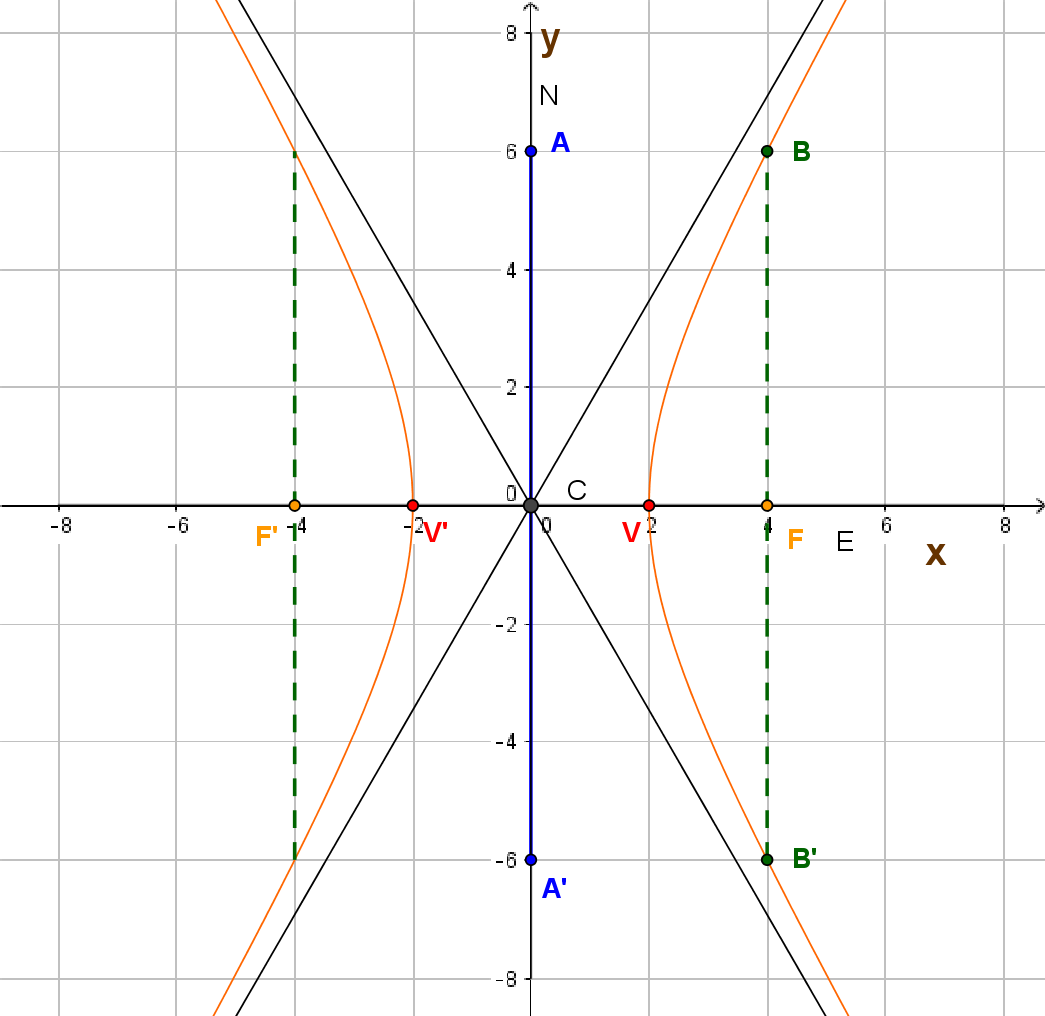
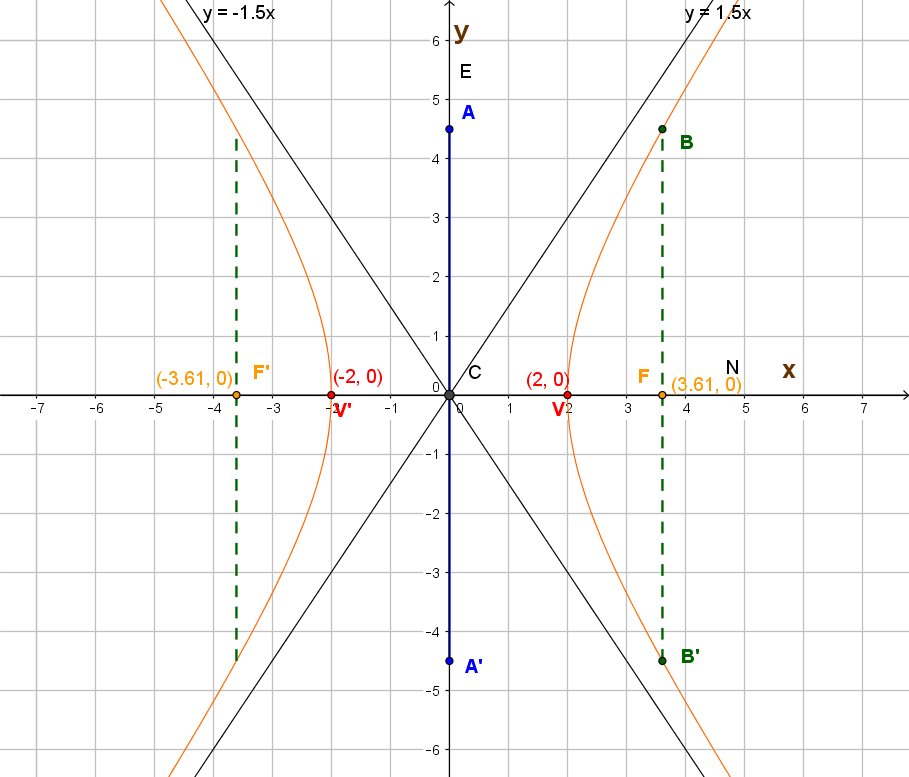
La hipérbola es el lugar geométrico del conjunto de puntos $P(x,y)$, tales que el valor absoluto de la diferencia de sus distancias a dos puntos fijos, llamados focos, es constante. Esta constante, denotada por $2a$, es la distancia entre sus vértices ($a:$ es la distancia entre el centro y cualquiera de los vértices). Su representación en el plano cartesiano es la siguiente. Observa cada uno de sus elementos:

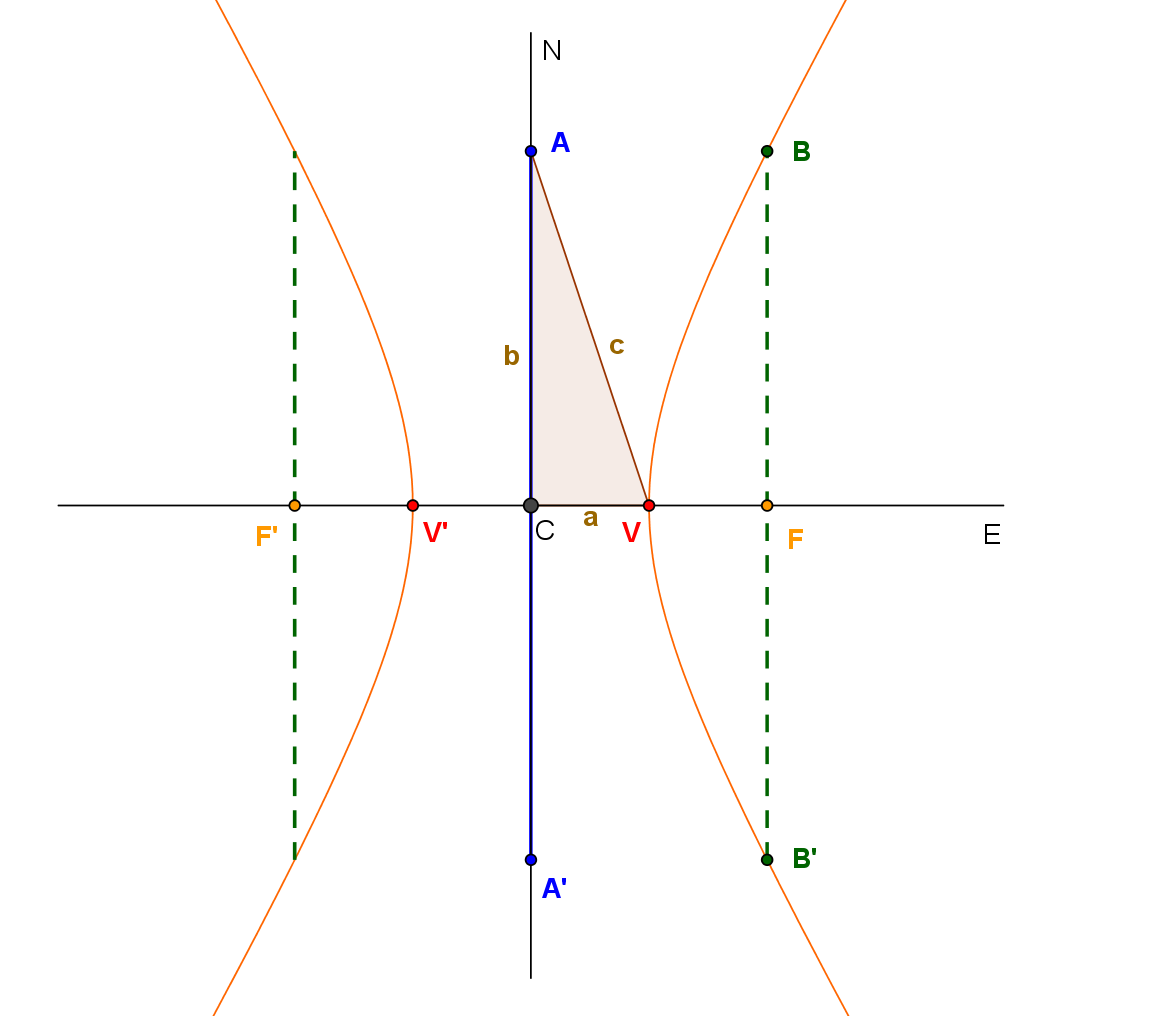
E=Eje focal

N=Eje normal

C=Centro

F, F'=Focos

V,V'= Vértices

$\overline{(AA')} $ = Eje conjugado

$\overline{(VV')}$ = Eje Transverso

$\overline{(BB')}$ = Lado recto

Observa en la figura que el triángulo $\Delta AVC$ es rectángulo: las longitudes de sus sus catetos son $a$ y $b$ y la de su hipotenusa $c$. Estas tres longitudes son las que definen los elementos de la hipérbola y con ellas obtenemos su ecuación, aplicando el Teorema de Pitágoras.
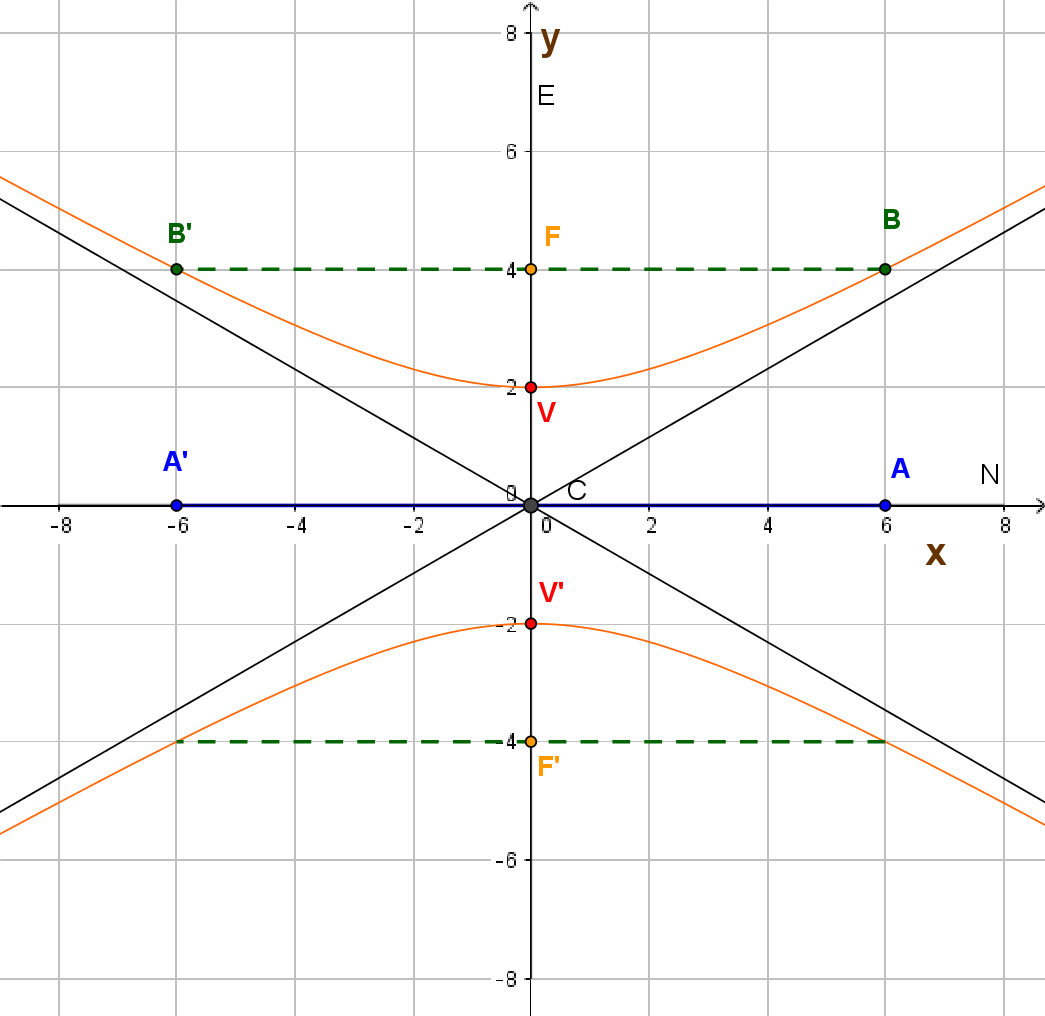
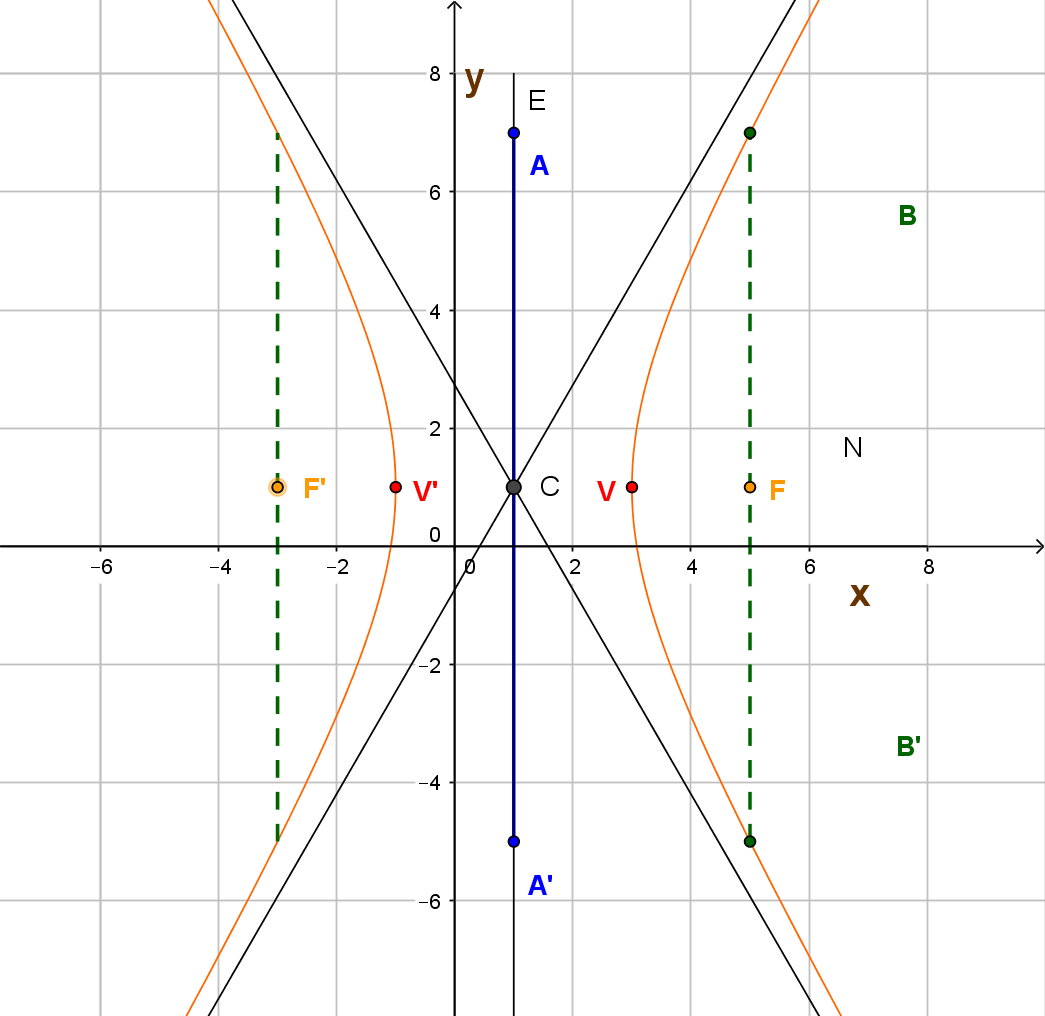
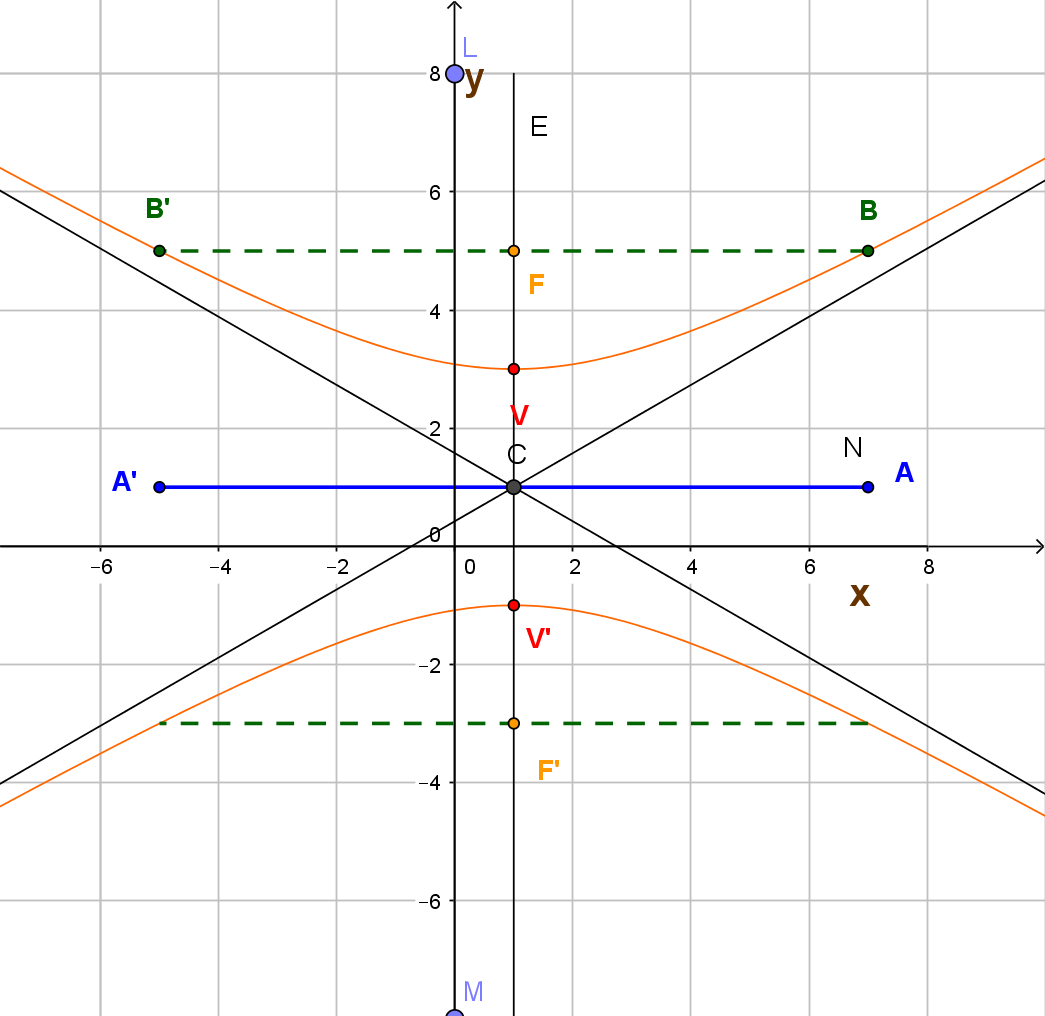
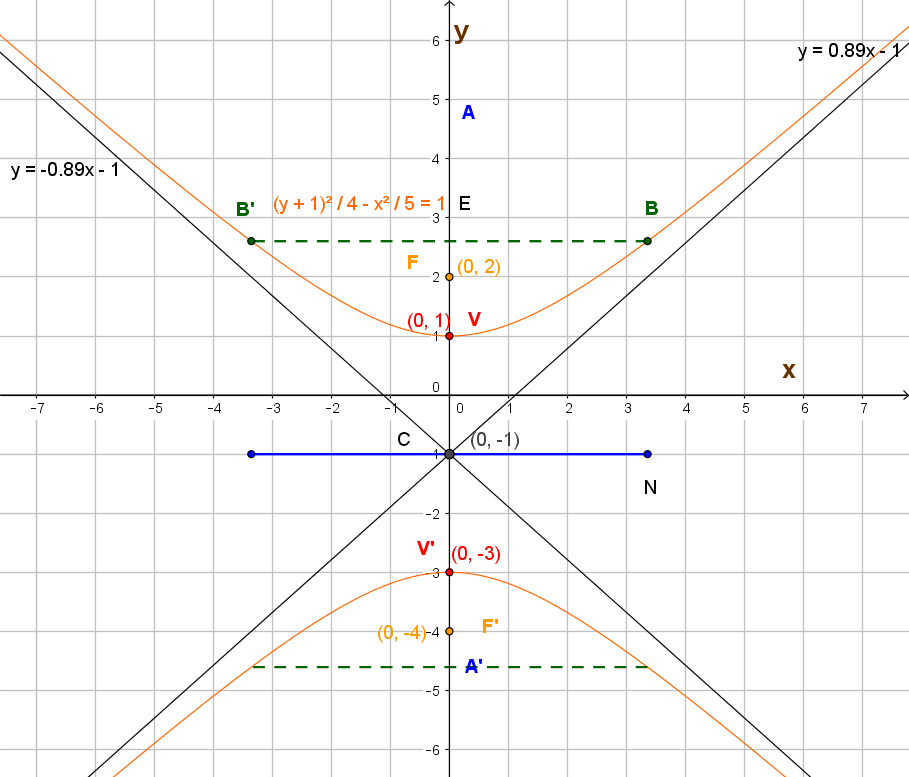
El centro de la hipérbola es el punto de intersección entre el eje focal (segmento que une a sus dos focos) y el eje normal (segmento perpendicular al eje focal que pasa por el centro). Aquí estamos describiendo hipérbolas con centro en el origen y eje focal paralelo a los ejes cartesianos. La hipérbola se llama horizontal si su eje focal es paralelo al eje $x$ y vertical si su eje focal es paralelo al eje $y.$
Las ecuaciones de estas hipérbolas son: $$\frac{x^2}{a^2}-\frac{y^2}{b^2}\qquad \text{ (para hipérbolas horizontales como la de la figura)}$$ y $$\frac{y^2}{a^2}-\frac{x^2}{b^2}\qquad \text{ (para hipérbolas verticales)}$$ El eje transverso (o transversal), es el segmento que une a los dos vértices de la hipérbola, mide $2a$ y el eje conjugado, cuya medida es $2b$, es perpendicular al eje transverso y pasa por el centro de la hipérbola.
La distancia entre los focos se llama distancia focal o eje focal y su medida es $2c.$ La hipérbola tiene dos lados rectos

Una hipérbola de centro en el origen y ejes paralelos a los cartesianos, puede ser vertical u horizontal dependiendo de si su eje focal es paralelo al eje $x$ o al eje $y.$

La hipérbola es el lugar geométrico del conjunto de puntos $P(x,y)$, tales que el valor absoluto de la diferencia de sus distancias a dos puntos, llamados focos, es constante.

$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$

asíntotas y=±$\frac{b}{a}$ x

Hipérbola horizontal

$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1$

asíntotas y=±$\frac{a}{b}$ x

Hipérbola vertical

El centro podría ser un punto distinto al origen. Sea $C(h,k)$ el centro de la hipérbola. Si el eje focal es paralelo a los ejes coordenados, entonces hay dos posibles ecuaciones dependiendo de si la hipérbola es horizontal o vertical:

$\frac{(x-h)^2}{a^2}-\frac{(y-k)^2}{b^2}=1$

asíntotas: $y-k=± \frac{b}{a} (x-h)$

Hipérbola horizontal

$\frac{(y-k)^2}{a^2}-\frac{(x-h)^2}{b^2}=1$

asíntotas: $y-k=±\frac{a}{b} (x-h)$

Hipérbola vertical

Ejemplo

1. Hallar los elementos y graficar la hipérbola cuya ecuación es: $\frac{x^2}{4}-\frac{y^2}{9}$ = 1

Corresponde a la ecuación $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ y, por lo tanto:

Si $a^2=4 ⇒a=2$

Si $b^2=9 ⇒b=3$

Si $c^2=a^2+b^2$

$c^2=4+9=13 ⇒ c=\sqrt{13}$

Por lo tanto sus elementos son:

Centro: C(0,0)

Focos:

F(c,0)=F($\sqrt{13},0$)

F'(-c,0)=F'(-$\sqrt{13},0$)

Vértices:

V(a,0)=V(2,0)

V'(-a,0)=V'(-2,0)

LLR=$\frac{(2b)^2}{a}=\frac{2(3)^2}{2}=\frac{2(9)}{2}=\frac{18}{2}=9$

e=$\frac{c}{a}=\frac{ \sqrt{13} }{ 2 }$

asíntotas y=±$\frac{b}{a}x ⇒ y=±\frac{3}{2}x$

2. Hallar los elementos y la gráfica de la hipérbola con centro en el punto C(0,-1) , uno de sus vértices es el punto V(0,-3) y la longitud del lado recto es 5.

Como el eje focal es paralelo al eje de las ordenadas, entonces la ecuación es de la forma: $\frac{(y-k)^2}{a^2}-\frac{(x-h)^2}{b^2}=1$

Se sabe que la longitud del lado recto es 5 y las coordenadas del centro son C(0,-1), entonces:

La distancia del centro al vértice es el parámetro a, entonces:

$a=2⇒a^2=4$

Si LLR=5 , entonces:

$\frac{(2b)^2}{a}=5$

$\frac{(2b)^2}{2}5,(2b)^2$=$5(2),(2b)^2$=$10,b^2$=$\frac{10}{2}⇒ b^2=5$

Calculando c:

Si $c^2=a^2+b^2$

$c^2=4+5=9 ⇒ c$=$\sqrt{9}=3$

$e=\frac{3}{2}$

asíntotas: $y-k=±\frac{a}{b} (x-h)$, $y-(-1)$=$±\frac{2}{\sqrt{5}} (x-0)$, $y+1$=±$\frac{2}{\sqrt{5}}x$

Como el centro de la hipérbola es C(0,-1) , entonces la ecuación es:$\frac{(y+1)^2}{4}-\frac{x^2}{5}=1$

Autoevaluación

1. Hallar los elementos y graficar la hipérbola cuya ecuación es: $\frac{x^2}{16}-\frac{y^2}{8}=1$
2. Hallar los elementos y graficar la hipérbola cuya ecuación es: $\frac{y^2}{16}-\frac{x^2}{64}=1$
3. Hallar los elementos y graficar la hipérbola cuya ecuación es: $\frac{x^2}{16}-y^2=1$
4. Hallar los elementos y graficar la hipérbola cuya ecuación es: $\frac{(x+2)^2}{9}-\frac{(y-2)^2}{7}=1$
5. Hallar los elementos y graficar la hipérbola cuya ecuación es: $\frac{(y-1)^2}{9}-\frac{(x-1)^2}{16}=1$

Verifica tus resultados aquí class