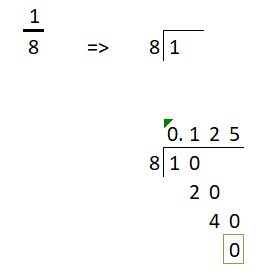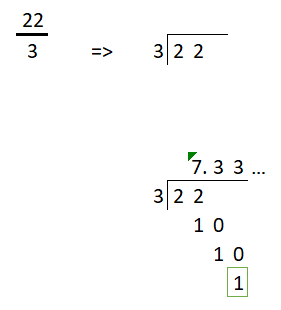¿Qué es un número racional?

Un número racional o fraccionario es aquel número que puede ser expresado como cociente de dos números enteros: $$\frac{a}{b}$$

en esta expresión $a$ y $b$ son números enteros y $b \neq 0$. Frecuentemente, los números racionales se usan para indicar que algo ha sido dividido en partes más pequeñas.

Por ejemplo cuando partes una pizza en rebanadas. Al partir un círculo en tres partes, el área de cada parte, podría ser expresada con un número racional.

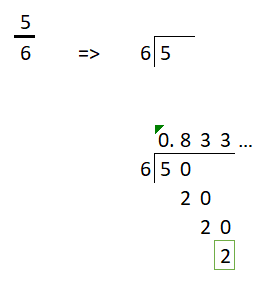
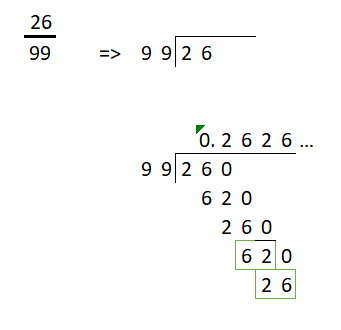
Existen dos formas de representar un número racional:

de forma decimal o como una fracción

Aquí aprenderás a pasar de una representación a otra.

Representaciones de un número racional

Cualquier número racional puede ser expresado como un cociente de números enteros. De hecho, esta es la causa de que se llamen racionales pues este término proviene de razón que es otra forma de referirse al cociente de dos números.

Ejemplos:

$$ \frac{1}{3} \quad \quad \frac{22}{7} \quad \quad \frac{3}{5} $$

El número de arriba de la línea lleva el nombre de numerador y el de abajo se llama denominador.

Otra forma de expresar un número racional es usando la notación decimal, es decir, mediante un número con parte entera, luego un punto, el punto decimal, -aunque hay quienes utilizan una coma- y luego la parte decimal, expresada por los dígitos después del punto decimal.

Representación decimal

De esta forma de escribir racionales hay dos casos posibles:

1. Que el número tenga parte decimal finita:

   Es decir, los dígitos que forman la parte decimal, se acaban.

   Ejemplos:

   $$ 3.45 \quad \quad 2.78475 \quad \quad 8.92$$

2. Que el número tenga parte decimal infinita:

   En este caso, la parte decimal del número no se puede expresar con una cantidad finita de dígitos, es decir, no se acaban. Entonces, la parte decimal se extiende indefinidamente pero, existe un patrón numérico que se repite periódicamente.

   Esto significa, que hay una colección de dígitos que aparecen una primera ocasión y, al terminar, vuelve a aparecer, al terminar esta segunda, vuelve a aparecer y así hasta infinito.

   Por ejemplo, el número $\dfrac{1}{3}$ cuya expresión decimal es $0.33333333….$ tiene una infinidad de números “$3$”, su parte decimal es infinita pero periódica, pues se repite indefinidamente.

   En estos casos, para no escribir tantos números, denotamos el patrón numérico que se repite colocándole una barra encima, así, expresaremos a este número como $0.\overline{3}$

   Los dígitos que se repiten están bajo la barra.

   Decimos entonces que el número tiene una expresión periódica infinita.

   Ejemplos:

   $$ 5.\overline{7} \quad \quad 32.\overline{25} \quad \quad 0.012\overline{4598}$$

Estudiaremos las dos representaciones de números racionales y verás que fácilmente puedes pasar de una a otra.

De fracciones a decimales

Si tenemos un número expresado en forma de fracción podemos expresarlo en forma decimal.

Para hacerlo, hacemos la división que la fracción indica: el denominador es el divisor y el numerador es el dividendo.

Ejemplo: $$ \frac{1}{8} = 0.125 $$

Fuente: Wikimedia Commons

Sin embargo, hay fracciones en las que al efectuar la división, no se llega nunca a residuo cero. Es así como se obtienen expresiones periódicas infinitas.

Así, tenemos que:

Observa que, como los residuos se repiten, las expresión decimal se extenderá de forma infinita pero repitiendo periódicamente las mismas cifras.

Estos son otros ejemplos:

$$ \frac{22}{3} = 7.\overline{3} $$

$$ \frac{5}{6} = 0.8\overline{3} $$

$$ \frac{26}{99} = 0.\overline{26} $$

En estos casos la expresión periódica infinita de estos números son $3$ en los primeros dos ejemplos y $26$ en el último.

De decimales a fracciones

Ahora, dado un número escrito en forma decimal existen distintas formas para conocer su expresión como fracción. Hay que considerar distintos casos.

• Si el número tiene parte decimal finita, -sus cifras decimales se terminan- entonces, hay que buscar una potencia de $10$ conveniente. ¿Qué significa esto? recuerda que al multiplicar un número decimal por $10$ el punto decimal se recorre una posición a la derecha. Por ejemplo $$167.095 \times 10= 1670.95$$ y al multiplicarlo por $100$ se recorre dos posiciones a la derecha $$167.095 \times 100 = 16709.5$$ y si lo multiplicamos por $1000$ $$167.095 \times 1000 = 167095$$ de esta expresión podemos “despejar” el número con el que iniciamos para obtener que: $$167.095 = \frac{167095}{1000}$$

  Sencillo, ¿cierto?

  Entonces, buscar una potencia de $10$ conveniente significa encontrar esa potencia de diez por la cual hay que multiplicar el número para convertirlo en un número entero, es decir, para recorrer el punto hasta la última cifra de su parte decimal.

  Otro ejemplo:

  $$0.17892 = \frac{17892}{100000}$$

• Si el número dado tiene parte decimal infinita, -sus cifras decimales no terminan- en este caso utilizamos el siguiente algoritmo, que ejemplificamos en cada paso.

  Considera el número $12.42333...= 12.42\overline{3}$:

  
  
  
  1. a. Comenzamos identificando la expresión periódica infinita.

     en este caso es $\overline{3}$

  2. b. Consideramos el número formado por: la parte entera junto con las cifras previas a la expresión periódica infinita y las de un período, $$\text{en este caso }12423$$
  3. c. A este número le restamos el número formado por la parte entera y las cifras decimales que no pertenecen a la expresión periódica infinita. Este será el numerador: $$12423-1242=11181$$
  4. d. En el denominador colocamos tantos nueves como dígitos contiene la expresión periódica infinita, seguidos de tantos ceros como dígitos hay en la parte decimal que no pertenece a la expresión periódica infinita. Para este ejemplo: $$900$$
  5. e. El resultado será: $$\frac{11181}{900}$$

Revisemos más ejemplos.

Consideremos el número:

$$5.\overline{74}$$

Siguiendo los pasos del algoritmo:

1. Comenzamos identificando la expresión periódica infinita, que es $\overline{74}$
2. Consideramos el número formado por la parte entera junto con las cifras previas a la expresión periódica infinita y las de un período: $$\text{en este caso }574$$
3. A este número le restamos el número formado por la parte entera y las cifras decimales que no pertenecen a la expresión periódica infinita, este será el numerador buscado: $$574-5=569$$
4. En el denominador colocamos tantos nueves como dígitos tiene expresión periódica infinita, seguidos de tantos ceros como cifras hay en la parte decimal que no pertenece a la expresión periódica infinita. Para este ejemplo: $$99$$

   Entonces tenemos:

   $$5.\overline{74}= \frac{574-5}{99}=\frac{569}{99}$$

Un ejemplo más. Consideremos el número:

$$0.397272...= 0.39\overline{72}$$

1. Comenzamos identificando la expresión periódica infinita, que es $\overline{72}$
2. Consideramos el número formado por la parte entera junto con las cifras previas a la expresión periódica infinita y las de un período: $$\text{en este caso }3972$$
3. A este número le restamos el número formado por la parte entera y las cifras decimales que no pertenecen a la expresión periódica infinita, este será el numerador buscado: $$3972-39=3933$$
4. En el denominador colocamos tantos nueves como dígitos tiene expresión periódica infinita, seguidos de tantos ceros como cifras hay en la parte decimal que no pertenece a la expresión periódica infinita. Para este ejemplo: $$9900$$

   Entonces

   $$ 0.397272...= 0.39\overline{72} = \frac{3972-39}{9900} = \frac{3933}{9900} = \frac{437}{1100} $$

Un último ejemplo para que quede totalmente claro. Consideremos el número:

$$0.294639639...= 0.294\overline{639}$$

1. Comenzamos identificando a expresión periódica infinita, que es $\overline{639}$
2. Consideramos el número formado por la parte entera junto con las cifras previas a la expresión periódica infinita y las de un período: $$\text{en este caso }294639$$
3. A este número le restamos el número formado por la parte entera y las cifras decimales que no pertenecen a la expresión periódica infinita, este será el numerador buscado: $$294639-294=294345$$
4. En el denominador colocamos tantos nueves como dígitos tiene expresión periódica infinita, seguidos de tantos ceros como cifras hay en la parte decimal que no pertenece a la expresión periódica infinita. Para este ejemplo: $$999000$$

   Entonces:

   $$ 0.294639639...= 0.294\overline{639} = \frac{294639-294}{999000} = \frac{294345}{999000} $$

Los racionales son precisamente los números que se pueden expresar como cociente de dos números enteros. Si un número real no se puede expresar de esta forma entonces no es un racional, estos números se conocen como irracionales.

Los irracionales tienen la característica de que en su representación decimal, la parte decimal se extiende de manera infinita sin presentar un patrón de repetición periódica.

Ejemplos de estos números: son $\pi$, $e$ y la raíz cuadrada de $2.$

¿Sabías que entre 0 y 1 hay tantos racionales como números enteros?

Se pueden contar de la siguiente forma:

Autoevaluación

Resuelve lo siguiente: