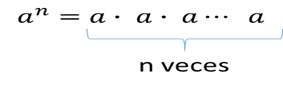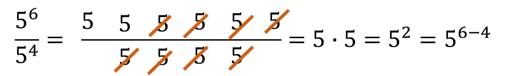Las ventajas de usar exponentes

En la simbolización matemática, los exponentes representan una invaluable ayuda en la escritura de números muy grandes o muy pequeños.

Pensemos en la representación de $10^n$, esto significa multiplicar $n$ veces el $10$ por sí mismo, por lo que como resultado, se tendrá un $1$ seguido de $n$ ceros. ¿Y que significa $a^n$, si $a$ es un número real distinto de cero y $n$ es un entero positivo? (Observa que si $a$ fuera cero entonces el resultado siempre sería $0$).

El número $n$ nos indica el número de veces en que se multiplica $a$ por sí mismo. Al número $a$ le llamamos base, y a $n$ exponente, entonces,

Ejemplos

Supongamos por ejemplo, que $a = 5$, vamos a multiplicar y dividir potencias con base $5$.

Multiplicación

Observa que entonces, $5^m \cdot 5^n = 5 ^{m+n}$ para cualquier par de enteros positivos $m,n.$

División

Observa que entonces, $\dfrac{5^m}{5^n} = 5 ^{m-m}$

O sea que para potencias de base 5, se cumple que:

• Al multiplicarlas se suman los exponentes.
• Al dividirlas se restan los exponentes.

Para verificar esta conclusión puedes auxiliarte de una calculadora, o bien de una tabla de potencias de 5. Veamos cómo usarla.

En el primer ejemplo vimos que $5^2 \cdot 5^4 = 5 ^{6}$. Comprobemos:

Entonces, nuestro resultado es correcto.

Los negativos no se discriminan

Pero, ¿qué sucede cuando los exponentes son enteros negativos? para eso usamos la siguiente definición: si tenemos cualquier número real $a$ diferente de cero y $n$ es un número natural, entonces $$a^{-n}=\frac{1}{a^{n}}$$

Los exponentes negativos los usamos para expresar números muy pequeños que nos permiten representar situaciones microscópicas. Al hacer operaciones con ellos, no cambian las reglas, es decir, en la multiplicación también sumamos los exponentes y en la división los restamos. Debemos tener cuidado con el manejo de los signos.

De hecho, las propiedades de los exponentes que hemos visto, se cumplen para cualquier número real $a\neq 0$ que elijamos como base, y para cualquier pareja de números enteros $m$ y $n$, por esto se les conoce con el nombre de leyes de los exponentes.

Las leyes de los exponentes

Si $a$ y $b$ son números reales y $m$ y $n$ dos enteros, entonces:

• 1. $a^m \times a^n = a^{m+n}$
• 2. $\dfrac{a^m}{a^n} = a^{m-n}$ con $a ≠ 0$
• 3. $(a^m)^n = a^{mn}$
• 4. $(a \times b)^n = a^n \times b^n$
• 5. $\left(\dfrac{a}{b}\right)^n = \dfrac{a^n}{b^n}$ con $b ≠ 0$

Observa la segunda ley $$\dfrac{a^m}{a^n} = a^{m-n}$$ ¿qué sucede si $m = n$? lo veremos con un ejemplo.

Supongamos que $a=3$ y $m=n=8$, aplicando la 2ª ley: $$\frac{3^8}{3^8} = 3^{8-8} = 3^0$$

Pero por otro lado sabemos que cualquier número diferente de cero entre sí mismo, da uno. Es decir: $1 = \frac{3^8}{3^8}$ por lo tanto $1 = 3^0.$

Así, la segunda ley nos permite definir lo que significa que cualquier número (diferente de cero) esté elevado al exponente cero: $$\text{Si } a \neq 0 \text{ entonces } a^{0}=1$$

Entonces, hemos definido lo que significa la potencia de un número, cuando el exponente es cualquier número entero, ya sea positivo, negativo o cero.

¿Qué nos dice la tercera ley? $$(a^m)^n = a^{mn}$$ Si tenemos una potencia cuya base es a la vez otra potencia, entonces para simplificarla sólo tenemos que multiplicar los exponentes. Es decir, si tenemos $$(a^3)^4 = a^{3 \times 4} = a^{12}$$

Revisa en los siguientes ejemplos la aplicación de las demás leyes de los exponentes:

Ahora apliquemos lo que has aprendido. Simplifiquemos el cociente: $$\frac{50^{50}}{25^{25}}$$

Hay que descomponer el exponente $50$ para poder aplicar la 5ª ley: $$50^{50} = 50^{25} \, \times \, 50^{25}$$

$$\Rightarrow \frac{50^{50}}{25^{25}} = \frac{50^{25} \times 50^{25}}{25^{25}} = \frac{50^{25}}{1} \times \frac{50^{25}}{25^{25}} = $$ $$=50^{25} \times \left(\frac{50}{25}\right)^{25} = 50^{25} \times 2^{25} = (50 \times 2)^{25} = 100^{25}$$

Autoevaluación

Esperamos que estos conocimientos te sean útiles. Para verificar que los has aprendido te invitamos a realizar la siguiente evaluación. Relaciona las columnas de acuerdo al resultado correcto.