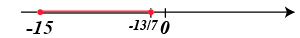Intervalos
Los intervalos son conjuntos de números reales. Corresponden geométricamente a rectas, semirrecta y segmentos de recta. De la misma manera que los conjuntos, es posible aplicarles las operaciones de unión, intersección y complementación.
Estos conjuntos aparecen con frecuencia en el estudio de las propiedades de los números reales y por tanto también cuando se estudian funciones reales o cálculo diferencial e integral. Permiten manejar con más comodidad conjuntos infinitos.
Para las definiciones siguientes estaremos suponiendo que $a,b\in \mathbb{R}$ con $a < b$. Revisaremos primero los intervalos acotados.
Intervalos acotados
Intervalos abiertos
Un intervalo abierto es un conjunto definido como: $$(a,b)=\{x \in \mathbb{R} | a < x < b\}$$
Observa que de esta definición se desprende que $a \notin (a,b)$ y $b \notin (a,b)$. Entonces, este intervalo contiene a todos los números reales que están entre $a$ y $b$ pero sin $a$ ni $b$.
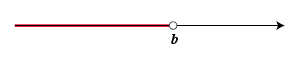
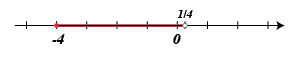
Geométricamente, este conjunto en la recta real, se ve como un segmento de recta sin los extremos (que se colocan como círculos vacíos en los puntos correspondientes).

Intervalo cerrado
Un intervalo cerrado es un conjunto definido como: $$[a,b]=\{x \in \mathbb{R} | a \leq x \leq b\}$$
Observa que para este caso $a \in [a,b]$ y $b \in [a,b]$. Es decir, el intervalo contiene a $a,$ $b$ y a todos los números reales que están entre ellos.
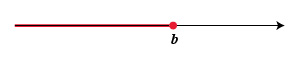
Geométricamente, este conjunto en la recta real, se ve como un segmento de recta incluyendo sus extremos (que se colocan como círculos llenos en los puntos correspondientes).

También existen las combinaciones posibles de estos dos tipos de intervalos.
Intervalo semiabierto
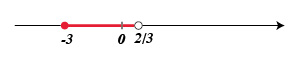
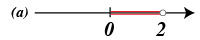
Es un intervalo que incluye solamente a un extremo. En este caso, cerrado por la izquierda, abierto por la derecha.
$$[a,b)=\{x \in \mathbb{R} | a \leq x < b\}$$

$a \in [a,b)$ y $b \notin [a,b)$
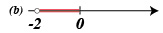
Ahora, definamos el intervalo semiabierto que es abierto por la izquierda y cerrado por la derecha.
$$(a,b]=\{x \in \mathbb{R} | a < x \leq b\}$$

$a \notin (a,b]$ y $b \in (a,b]$
Como puedes observar, en la notación de intervalos los paréntesis indican una desigualdad estricta, geométricamente se especifica el punto no incluido con un círculo vacío; mientras que los corchetes definen una desigualdad débil que sí incluye al punto extremo y geométricamente se dibuja con un círculo lleno.
Los intervalos definidos hasta aquí son acotados, porque en todos los casos sus extremos son números reales. Como vimos, su representación geométrica corresponde a un segmento de recta, con o sin extremos.
Observaciones importantes:
• Si $a > b$ los intervalos, así como los definimos, no contendrían elementos y entonces representarían al conjunto vacío, $\emptyset$.
• $(a,a), [a,a)$ y $(a,a]$ también representan al conjunto vacío.
• El intervalo $[a,a]$ describe al conjunto $\{a\}$ formado por un solo elemento.
• La notación $(a,b)$ es usada en otras áreas de las matemáticas para describir otros conceptos -pares ordenados en el plano cartesiano, máximo común divisor de dos números, números complejos, vectores- esto suele ocurrir y sin embargo no debería causar confusión pues el contexto en el que se use te permitirá entender cuál de los conceptos está representando.
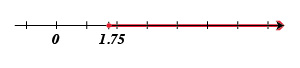
• Existen además los intervalos no acotados.