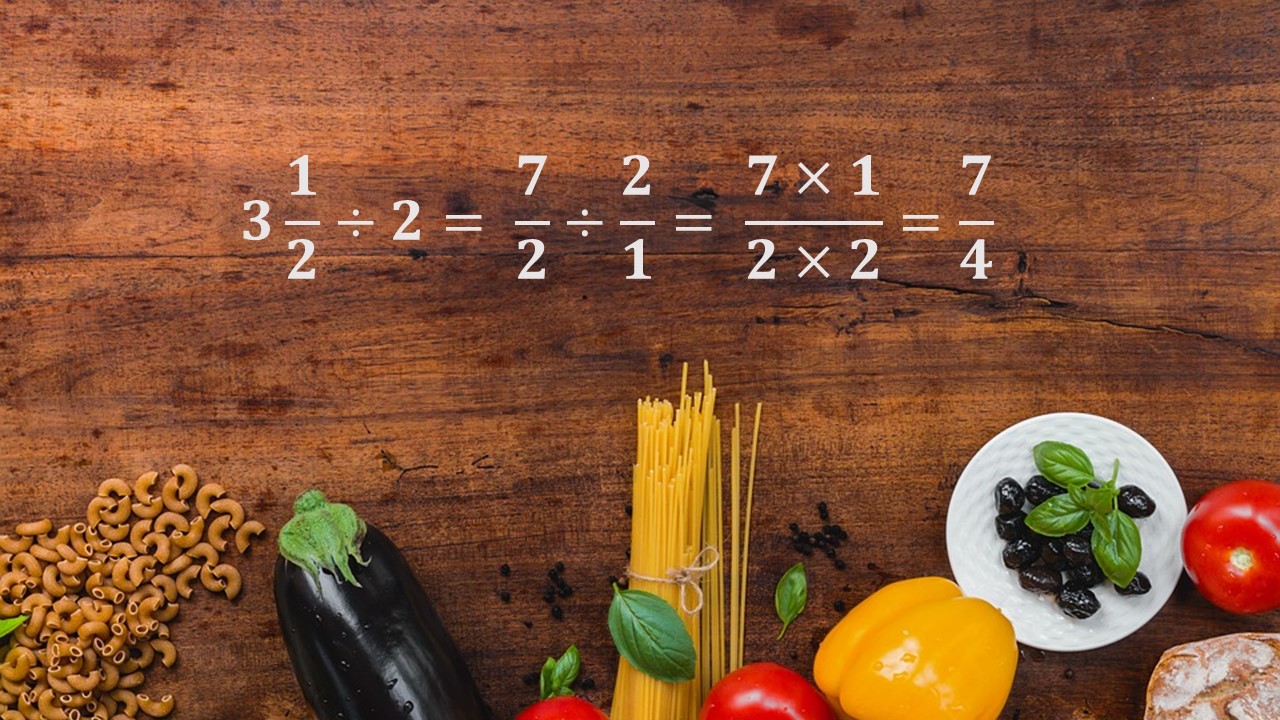¿Cómo divides una parcela?

Imagina que eres dueño de una parcela en la que quieres construir tu casa y para poder lograrlo necesitas vender la cuarta parte y del restante rentar la tercera parte, en el espacio que queda, es donde construirás tu hogar. Si sabes que tu parcela es de $1000\:m^2$, la pregunta inmediata es ¿cuántos metros cuadrados quedan para poder realizar la construcción?

Para poder contestar esta pregunta y muchas otras, es necesario saber realizar operaciones con números fraccionarios. ¡Vamos a aprender!

¿Qué es el mínimo común múltiplo de dos números?

Antes que nada, recordemos que un múltiplo común de dos o más números es aquel número que contiene exactamente a cada uno de ellos. Por ejemplo, $90$ es múltiplo común de $6$ y $10$, porque $90$ contiene exactamente $15$ veces al $6$ y $9$ veces al $10$.

Llamamos mínimo común múltiplo de dos o más números, al menor número que contiene a cada uno de ellos un número exacto de veces y se denota por m.c.m.

La forma más común de hallar el m.c.m. de dos o más números es descomponer cada uno de ellos en sus factores primos, el m.c.m. se forma con el producto de los factores primos elevados a su mayor exponente.

A continuación se presentan un par de ejemplos.

1. Hallar el m.c.m. de $50$ y $80$

1. Hallar el m.c.m. de $80$, $120$ y $300$

El objetivo de esta UAPA es aprender a operar con fracciones, por ello no se ahonda más en cómo obtener el m.c.m. pero, si necesitas más ayuda puedes revisar la uapa Mcd y Mcm.

Suma y resta de fracciones

Los procedimientos para sumar o restar fracciones son muy similares. Distinguiremos varios casos:

Caso 1. Fracciones con igual denominador

La regla para este caso es hacer las operaciones indicadas con los numeradores y conservar el denominador. El resultado se reduce, si es posible.

Ejemplo:

$$\frac{2}{3} + \frac{6}{3} + \frac{22}{3}= \frac{2+6+22}{3} = \frac{30}{3} = 10 $$

$$\frac{22}{23} - \frac{26}{23} = \frac{22-26}{23} = \frac{-24}{23} = -\frac{24}{23} $$

$$-\frac{2}{15} + \frac{7}{15} - \frac{10}{15}= \frac{-2+7-10}{15} = \frac{-5}{15} = -\frac{5}{15}= -\frac{1}{3} $$

Caso 2. Fracciones con distinto denominador

En este caso primero se reducen las fracciones de ser posible, luego se toman los denominadores y se les calcula su mcm Después, se reexpresa cada uno de los operandos pero con el denominador común y finalmente se procede a realizar las operaciones como en el caso anterior. Mira algunos ejemplos:

$$\frac{4}{5} + \frac{6}{8} $$

el mcm de 5 y 8 es 40. Al reexpresar la operación con este denominador, obtenemos:

$$\frac{4}{5} + \frac{6}{8} = \frac{32}{40} + \frac{30}{40}= \frac{32+30}{40} = \frac{62}{40} = \frac{31}{20} $$

$$\frac{14}{10} + \frac{4}{6} - \frac{13}{5} $$

el mcm de 10, 6 y 5 es 30, luego:

$$\frac{14}{10} + \frac{4}{6} - \frac{13}{5} = \frac{42}{30} + \frac{20}{30} - \frac{78}{30} =\frac{30+20-78}{30} = -\frac{16}{30} $$

Mira más ejemplos, en los que por simplicidad se han omitido algunos pasos:

$$-\frac{5}{3} + \frac{4}{6} - \frac{23}{9} = \frac{-30+12-46}{18} -\frac{64}{18} = -\frac{32}{9} $$

$$\frac{1}{2} + \frac{2}{3} - \frac{3}{4} = \frac{6+8-9}{12} = \frac{5}{12} $$

Caso 3. Fracciones mixtas

Para este caso, se suman por separado los enteros y las fracciones, el resultado final es la suma de los resultados anteriores, solo hace falta asegurarse de reducir el número. Por ejemplo:

$$1\frac{3}{4}+10\frac{1}{2} = (1+10) + \left(\frac{3}{4} +\frac{1}{2}\right) = 11 + \frac{5}{4} = 12\frac{1}{4} $$

$$4\frac{2}{4}-5\frac{3}{2} = (4-5) + \left(\frac{2}{4} -\frac{3}{2}\right) = -1 - \frac{4}{4} = -2 $$

Ejemplo práctico:

Imagina que tienes cierta cantidad de dinero y decides ir al cine, si las entradas te cuestan la quinta parte del total de tu dinero y las palomitas la octava ¿Qué fracción de dinero te sobra?

¡Te sobran $\dfrac{27}{40}$ de tu dinero! ¿Es suficiente para mirar otra película?

Producto de fracciones

Cuando se trata de multiplicar quebrados ¡La regla es muy sencilla! Solo debes expresar todos los multiplicandos como fracciones propias. Después, se multiplican los numeradores y este producto se parte por el producto de los denominadores. El resultado se simplifica y se hallan los enteros si los hay.

Recuerda que los números enteros se pueden ver como fracciones cuyo denominador es uno.

Mira los siguientes ejemplos:

$$3 \times -\frac{3}{5} = \frac{3}{1} \times -\frac{3}{5} = \frac{3\times -3}{1\times 5} = \frac{-9}{5} = -1\frac{4}{5} $$

$$7\frac{1}{2}\times\frac{3}{4} = \frac{15}{2}\times\frac{3}{4}= \frac{15\times3}{2\times 4} = \frac{45}{8} = 5\frac{5}{8}$$

$$-\frac{2}{3}\times -\frac{3}{4} \times \frac{4}{5} = \frac{-2 \times -3 \times 4}{3 \times 4 \times 5} = \frac{24}{60} = \frac{2}{5} $$

$$1\frac{1}{3} \times 5 \times\frac{2}{4} = \frac{4 \times 5 \times 2 }{3 \times 1 \times 4} = \frac{40}{12} = \frac{20}{6}$$

Es muy fácil, ¿verdad?

Ejemplo práctico

Imagina que en la sala de cine hay $75$ personas, de las cuales dos terceras partes son adultos y de ellos, la mitad son varones ¿Cuántos adultos y cuántos adultos varones hay en la sala?

División de fracciones

Aunque en las actividades cotidianas es difícil que aparezcan divisiones de fracciones, éstas no dejan de ser útiles en diversas situaciones.

Realizar esta operación también es muy sencillo, aunque de forma directa funciona sólo de forma binaria (con dos operandos): se empieza por expresar cada fracción como una fracción propia y luego se multiplica el numerador de la primera por el denominador de la segunda y el resultado se coloca en el numerador. Después se multiplica el denominador de la primera con el numerador de la segunda y el resultado se coloca en el denominador. Finalmente se reduce el resultado de ser posible.

Es más sencillo entender esta operación con ejemplos:

$$\frac{3}{2}\div\frac{5}{7} = \frac{3 \times 7}{2 \times 5} = \frac{21}{10} = 2 \frac{1}{10}$$

$$3\frac{2}{6} \div -\frac{2}{3} = \frac{20}{6} \div -\frac{2}{3} = -\frac{20 \times 3 }{6 \times 2} = - \frac{60}{12}= -5$$

Si deseas dividir más de dos fracciones, debes hacerlo de forma binaria:

$$ \left( \frac{3}{2} \div \frac{4}{3}\right) \div \frac{5}{4} = \left( \frac{3\times 3}{2\times 4}\right) \div \frac{5}{4} = \frac{9}{8} \div \frac{5}{4} = \frac{9 \times 4}{8 \times 5} = \frac{36}{40} = \frac{9}{10}$$

Para ejemplificar esta operación, imagina que estás preparando una receta en la que $3$ tazas y media de pasta deben ser divididas en dos recientes ¿cuánta pasta debes agregar a cada uno de ellos?

Autoevaluación

Ahora que ya sabes realizar operaciones con quebrados, es tiempo de poner a prueba tus nuevos conocimientos: