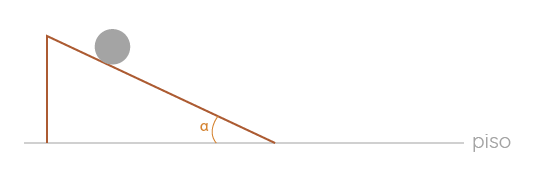
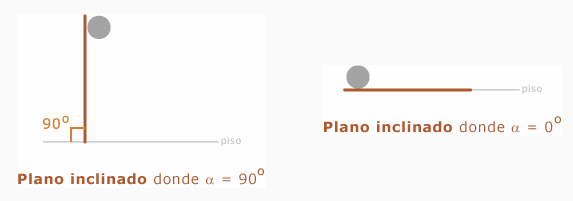
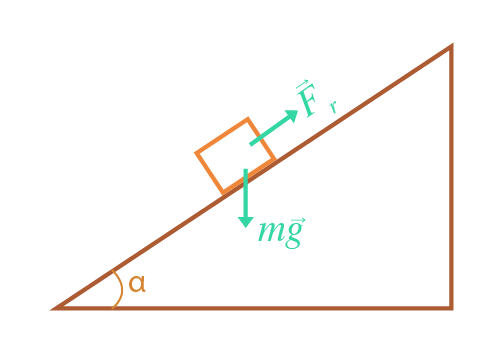
El plano inclinado (comúnmente conocido como rampa) consiste en una superficie recta que forma un ángulo con respecto a la horizontal y que desde hace mucho tiempo el hombre ha usado como una máquina simple de la que se ayuda para elevar cosas con mayor facilidad que si las alzara verticalmente. Sin embargo, esta máquina fue usada por Galileo Galilei con otros fines.

Como ya te habrás percatado, los cuerpos caen muy rápido para que nuestros sentidos detallen la trayectoria con precisión. Actualmente contamos con tecnología capaz de registrar con mucho detalle el desarrollo del movimiento en la caída de los cuerpos. Por ejemplo, contamos con cámaras fotográficas de gran rapidez con las que se obtienen impresiones nítidas de los objetos en caída.

También hay cámaras de video que nos permiten seguir en “cámara lenta” o bien “cuadro a cuadro” su comportamiento, además de que se cuenta con relojes muy precisos con los cuales podemos ser capaces de registrar tiempos de milésimas de segundo.

Pero en la época de Galileo (siglo XVII) ni siquiera se contaba con un reloj mecánico, de modo que este gran científico tuvo que ingeniárselas para poder analizar la caída de los cuerpos.

Antes de ver cómo fue que Galileo resolvió el problema te proponemos que pienses por un momento ¿cómo medía el hombre el tiempo antes de que se inventaran los relojes mecánicos? En épocas muy antiguas el tiempo se medía utilizando diversos instrumentos que presentan un ciclo más o menos constante. Por ejemplo, una de las primeras formas de medir el tiempo fue ayudándose del pulso de una persona, otra manera fue usando relojes de arena y otro método fue contando el número de gotas de agua que caían (a espacios de tiempo regulares) después de pasar por un filtro de piedras y/o arena (estos relojes se llaman clepsidras). Sin embargo, estos tipos de relojes no son adecuados ya que no son muy precisos y la caída de un cuerpo sigue siendo muy rápida para ellos.

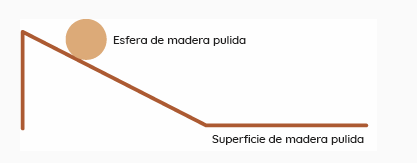
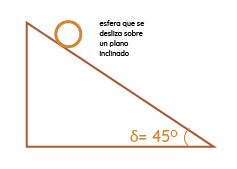
Con ello en mente Galileo pensó que la manera de disminuir la rapidez del movimiento sería “haciendo caer” al objeto a través de un plano inclinado. Con esto “atenuaría” la caída del objeto al modificar su trayectoria originalmente vertical a una trayectoria inclinada. Es obvio que la manera de razonar de Galileo estuvo basada en el método científico, por lo que, a diferencia de los romanos de la época clásica, Galileo realizó experimentos e hizo deducciones sobre lo que observó.

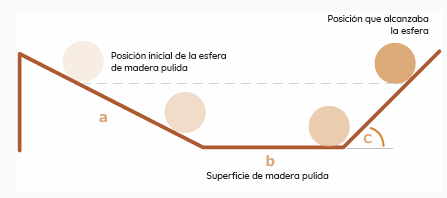
Se le ocurrió realizar experimentos con los cuales pudiera determinar si era o no cierta la suposición de que la fricción es la causa de que el objeto en movimiento se detenga.

Se sabe que en la época de Galileo ya había grandes artesanos en la madera y que Galileo utilizó esferas de madera muy bien pulidas, que hizo rodar sobre superficies lisas, también construidas de madera, como se observa en la siguiente figura.

Observó que, entre mejor pulidas estén las superficies en contacto (lo que significa que hay menos fricción), mayor tiempo perdura el objeto en movimiento.

Después modificó la trayectoria de la esfera, haciendo elevar un extremo (b) de la superficie, se dio cuenta que la esfera se detenía en un punto al mismo nivel que del que fue soltada, lo anterior sin importar cuan larga es la superficie (b) o el ángulo (c) al cual se inclina la superficie, claro que siempre menor que 90°.

Galileo entonces razonó de la siguiente manera: “si alargo demasiado la superficie (b) manteniéndola siempre horizontal y cuidando de que esté muy bien pulida, la esfera nunca se detendrá pues nunca alcanzará a altura de la cual fue lanzada inicialmente”.

Evidentemente, la esfera se llega a detener en algún momento porque siempre existe la fricción con la superficie y con el aire del ambiente (por más que se puedan minimizar ambas fricciones). Sin embargo, esta inferencia de Galileo sigue siendo extraordinaria porque le ayudó a imaginarse el comportamiento de los objetos en movimiento en un mundo sin fricción. De acuerdo a lo anterior debe suceder que: “un objeto en movimiento permanecerá en esa condición siempre y cuando no haya fuerza alguna sobre él que modifique dicho estado”, lo cual llevó muchos años para simularse experimentalmente.

Con estas conclusiones, Galileo echó por tierra, viejas y equivocadas ideas aristotélicas sobre el movimiento y dio paso a una nueva manera de ver al mundo. De hecho, Newton retomó esta última idea para concebir su ya famosa primera ley del movimiento que algunos también conocen con el nombre de ley de la inercia.

Como ya mencionamos, el plano inclinado es una superficie recta que forma un ángulo con respecto a la horizontal. Pues es precisamente este ángulo el que pudo variar Galileo con el fin lograr observar con mayor detalle la caída de un cuerpo. Aunque el fenómeno físico de que una esfera ruede cuesta abajo sobre un plano inclinado no implica una caída libre, sí se puede considerar como su representación en tanto que se trata de un objeto que está siendo permanentemente acelerado hacia el centro de la Tierra, por lo que aumenta su velocidad de manera uniforme.

Observa el esquema:

Nos damos cuenta de que en la construcción de un plano inclinado podemos decidir el valor del ángulo $\alpha$ en un intervalo abierto (0°,90°).

El intervalo es abierto ya que si elegimos el caso extremo donde $\alpha= 0°,$ entonces ya no tenemos plano inclinado, sino una superficie lisa continua, y la esfera que colocamos sobre ella no tendrá ninguna aceleración debido a la fuerza de gravedad. En cambio, si se elige el otro caso extremo donde $\alpha= 90°,$ entonces tampoco tendremos un plano inclinado sino más bien se trata de una caída libre de la esfera y volvemos al problema: resulta un movimiento de caída demasiado rápido para que podamos percibirlo directamente con nuestros sentidos.

Para comprender fácilmente algunos fenómenos físicos, algunas veces es conveniente analizar los casos extremos. Como te darás cuenta, en el caso extremo en que α = 90°, la caída será libre y el tiempo de caída está dado por:

$t=\sqrt{\frac{2d}{a} }$

Que resulta de despejar (t) a partir de la fórmula:

$d=V_0t+\frac{at^2}{2}$, ya que para este caso $V_0=0\frac{m}{s}$

Para el otro caso extremo, en que α = 0°, es evidente que el “tiempo de caída” se vuelve infinito ya que ¡nunca cae!

Conociendo los tiempos de caída para los casos extremos, sabemos que el tiempo de caída para cualquier ángulo en un intervalo abierto (0°,90°) tendrá un valor dentro del intervalo $(\infty,\sqrt{\frac{2d}{a}})$, pero para determinado ángulo α ¿cuál es el valor exacto de tiempo de caída (tα)?

El tiempo de caída de un cuerpo que se desliza sin fricción sobre un plano inclinado depende del ángulo al cual se encuentre el plano, de manera que: $t_∝=\frac{\frac{2d}{a}}{sen∝}$

Para tener una idea de cómo depende el tiempo de caída con el ángulo del plano inclinado te proponemos ver el siguiente ejemplo:

Supongamos que tenemos una canica a una altura de 4.9 m y la soltamos en caída libre. ¿Cuál es el tiempo de caída de la canica?

Recuerda que la distancia recorrida por la canica se considera negativa y que el tiempo de caída para un objeto en caída libre está dado por

$t=\sqrt{\frac{2d}{a}}$ = $\sqrt{\frac{2(4.9m)}{9.8\frac{m}{s}}}$ = $\sqrt{\frac{9.8m}{9.8\frac{m}{s}}}$=$\sqrt{1}=1s$

Ya vimos que este tiempo es el mínimo (pues se trata de una caída libre). Ahora, te presentamos la siguiente tabla con los valores del tiempo de caída de la canica a diversos ángulos de inclinación del plano.

¿Qué pasa cuando el ángulo se hace más pequeño? Reflexiona un poco.

Observaste que conforme el ángulo entre el plano y la horizontal se va haciendo cada vez menor, el tiempo va aumentando y como ya lo vimos para los casos extremos, si α = 90° estamos ante una caída libre (demora un segundo) y si α = 0°, estamos en el caso en que la canica está sobre una superficie horizontal y nunca cae (t α= ∞).

De esta forma (con una caída retardada) fue como Galileo pudo analizar con detalle la caída de los cuerpos y se dio cuenta que el objeto recorre en un segundo más distancia de la que había recorrido el segundo anterior debido a que adquiere más velocidad conforme transcurre el tiempo (a lo cual llamó aceleración). Este caso es un ejemplo de un MUA.

La aceleración

En los casos anteriores, no tomamos en consideración el peso del cuerpo, en este caso vamos a tomar en consideración el peso del objeto que va a deslizarse. Si un cuerpo se desliza sin rozamiento por un plano inclinado se mueve con una aceleración constante producida por la componente de la fuerza gravitacional al movimiento, es decir:

$F_g=mgsen\alpha$

Donde m es la masa del cuerpo que desliza sobre el plano inclinado y es el ángulo de inclinación. Si el ángulo de inclinación es 0° (cero grados), la suma de las fuerzas que actúan sobre el cuerpo se anula y éste permanece en reposo.

Veamos con más detenimiento estos datos. Sabemos que existe un peso que hace que nuestro “objeto” vaya hacia abajo, así como una fuerza que lo “jala” hacia la tierra conocido como gravedad. La flecha roja nos indica que existe un coeficiente de rozamiento.

En este caso, el coeficiente de rozamiento no es solicitado así que se tiene

$F=ma$

$F=mgsen\alpha$

Igualamos las F, y como lo que deseamos conocer son los datos de la aceleración, se tiene que $ma$=$mgsen\alpha$ cancelamos m de ambos lados y se tiene $a$=$gsen\alpha$

Donde g es la constante gravitacional

La aceleración debida a la fuerza de gravedad en un plano inclinado será entonces $a=9.8 \frac{m}{seg^2}sen\alpha$ y sin las unidades es $a=9.8sen\alpha$

Observemos el siguiente ejemplo ¿Cuál es la aceleración debido a la fuerza de gravedad de una esfera que se desliza sobre un plano inclinado (ver la figura de abajo), de manera que se puede considerar despreciable la fricción?

Sustituimos los datos

a=9.8 sen 45°

sen 45°=0.7071

a=(9.8$\frac{m}{seg^2}$)(0.7071)= 6.93 $\frac{m}{seg^2}$

Por lo que la aceleración es 6.93 $\frac{m}{seg^2}$

Autoevaluación

Esperamos que la explicación sobre el plano inclinado te haya resultado interesante. Para fortalecer tus avances, te pedimos realices el siguiente ejercicio:

Un transportista empuja una caja sobre un plano inclinado que forma un ángulo de 30° con la horizontal. La distancia de la caja hacia el piso es de 5 mts. El hombre recibe una llamada en su móvil y suelta la caja, la cual comienza a descender por la pendiente por la acción de su peso.

Te pedimos realices las siguientes actividades

1. Identifica todas las variables y datos necesario para resolver el problema
2. Calcula la aceleración de la caja en su huida, si no existe rozamiento.
3. ¿Cuánto tiempo tardará en llegar abajo?

Califica tus resultados de acuerdo a la siguiente rúbrica.class

Verifica resultados de acuerdo a la siguiente retroalimentación.class