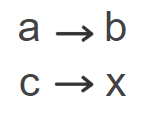¿Qué es proporcionalidad?

Uno de los conceptos matemáticos que tiene mayor alcance por su uso en la vida cotidiana es el de proporcionalidad; la cual se define como la relación entre dos magnitudes medibles.

Para entender mejor este concepto, debemos conocer otro, el concepto de razón. La razón entre dos números es simplemente el cociente que se obtiene de dividir uno entre otro, y se expresa como una fracción.

Una aclaración importante es que si alguno de los números es cero, como no es posible dividir entre éste, entonces cero no puede ser el denominador de la fracción (en particular, no es posible obtener la razón de 0 entre 0).

Si solamente uno de los números es cero, como el numerador sí puede ser cero, entonces la razón es cero. Y si tenemos que los números son $a$ y $b$, ambos distintos de cero, la razón entre ellos se representa como $$\frac{a}{b}$$

Revisemos algunos ejemplos:

Fuente: Pixabay

• Si en un grupo de amigos hay $6$ niños y $3$ niñas, la razón entre el número de niños y el número de niñas es: $$\frac{niños}{niñas} = \frac{6}{3}=\frac{2}{1}= 2$$

Fuente: Pixabay

• En un torneo de fútbol, un equipo ha anotado $29$ goles y recibido $18$. La razón entre goles anotados y goles recibidos es: $$\frac{\text{goles marcados}}{\text{goles recibidos}} = \frac{29}{18} = 1.6$$

Por supuesto hay distintas parejas de números con la misma razón. Por ejemplo, pensemos en algunas parejas de números cuya razón sea $2.5:$

$$5 \text{ y } 2\text{ y } 100\text{ y } 40\text{ y } 2.5\text{ y } 1$$

En efecto,

$$\frac{5}{2}=\frac{100}{40}=\frac{2.5}{1}=2.5$$

Decimos entonces que estas parejas de números son proporcionales entre sí.

Diremos entonces que los números $a$, $b$, $c$ y $d$ forman una proporción si la razón entre $a$ y $b$ es la misma razón que hay entre $c$ y $d$, es decir, si $$\frac{a}{b}=\frac{c}{d}$$ Las magnitudes proporcionales pueden ser directamente proporcionales o inversamente proporcionales.

¿Cuándo usamos la proporcionalidad?

Imagina que quieres preparar un pastel de chocolate para tus mejores amigos, por lo que le pides a tu abuela su receta que tanto te gusta. La receta es la siguiente:

Sin embargo, esta receta está redactada para $12$ personas y tú quieres hacerla para $4$, por lo que necesitas saber la proporción de ingredientes que vas a utilizar para no modificar el sabor de la receta original.

En este caso, hay una razón de $\frac{12}{4}=3$ entre la cantidad de personas de la receta original y la que tú vas a hacer, lo que quiere decir que el número de personas para las que está escrita la receta es $3$ veces mayor.

Entonces, la razón entre la cantidad indicada en la receta y las cantidades que usarás, debe ser $3$ para mantener la misma proporción; para ello se dividen las cantidades de cada ingrediente entre $3$.

Por ejemplo, si para $12$ personas necesitas $6$ huevos, para $4$ personas necesitarás $\frac{6}{3} = 2$ huevos. Revisa en la siguiente tabla la cantidad que necesitarás de cada ingrediente:

Ahora ya sabes lsa cantidades que debes utilizar para hacer un pastel para 4 personas, y puedes seguir los mismos pasos para hacer uno para la cantidad de personas que quieras, siempre que mantengas la proporción.

Proporcionalidad directa

Decimos que dos magnitudes son directamente proporcionales cuando al multiplicar o dividir una de ellas por un número, la otra queda multiplicada o dividida por ese mismo número.

Revisemos algunos ejemplos:

Fuente: Pixabay

• Cuando compras dulces, ¿qué relación hay entre la cantidad de dulces que compras y la cantidad de dinero que pagas por ellos? En la siguiente tabla se muestra el total que vas a pagar dependiendo de la cantidad de dulces que compres.

Dulces	Total a pagar
$1$	$\$5$
$3$	$\$15$
$5$	$\$25$
$10$	$\$50$

Notemos que la razón entre el total a pagar y la cantidad de dulces $\left(\frac{\text{total a pagar}}{\text{dulces}}\right)$ es $5$ en todos los pares de la tabla. Entonces, si tomamos como base que un dulce cuesta $\$5$, para saber cuánto es el total a pagar por $x$ número de dulces, se multiplica $\$5$ por $x$.

Por lo tanto, estas magnitudes son proporcionalmente directas.

Fuente: Pixabay

• Ahora pensemos en el recorrido de un automóvil por carretera a velocidad constante. Si la distancia aumenta, el tiempo que tome recorrerla aumentará proporcionalmente. En cambio si la distancia por recorrer disminuye, el tiempo que toma el recorrido disminuirá proporcionalmente.

Podemos concluir que el tiempo necesario para hacer el recorrido, es directamente proporcional a la distancia.

Regla de tres

Considera la siguiente situación:

Supongamos que Luis maneja a una velocidad constante y tarda una hora en llegar de su casa a Cuernavaca recorriendo un total de $150\:km$ , ¿cuánto tardaría en llegar a Querétaro si desde su casa son $230\:km$ de distancia?

Para resolver problemas de proporcionalidad directa como este, utilizamos la regla de tres directa.

Cuando conocemos dos magnitudes $a$ y $b$ que mantienen una relación de proporcionalidad directa y una de ellas varía, una regla de tres nos permite conocer el valor de la otra.

Para resolver una regla de tres, se colocan en una tabla, como se muestra a continuación, los datos que conocemos: $a$, $b$ y $c$ (la magnitud que varía); y la incógnita o dato que queremos averiguar a la cual llamamos $x$.

Con el ejemplo anterior:

$a = 150\:km$

$b = 60$ minutos

$c = 230\:km$

Esta tabla se lee de la siguiente forma: “$a$ es a $b$ como $c$ es a $x$”, lo que quiere decir que $a$ y $b$ son directamente proporcionales a $c$ y $x$. Para encontrar el valor de $x$ se usa la siguiente fórmula:

$$x = \frac{(c)\times(b)}{a}$$

En el ejemplo anterior:

$$x = \frac{(230)\times(60)}{150} = 92 $$

Es decir, Luis tardaría $92$ minutos en recorrer $230\:km$.

Revisemos otro ejemplo:

Ana quiere sorprender a su mejor amiga en su cumpleaños decorando el salón de clases con globos de colores. Si se tarda $18$ segundos en inflar dos globos, ¿cuánto tiempo le tomará inflar $50$ globos?

Los datos que tenemos son:

$a = 2$ globos

$b = 18$ segundos

$c = 50$ globos

Sustituyendo en la fórmula:

$$x = \frac{(50)\times(18)}{2} = 450 $$

Por lo tanto, Ana tardará $450$ es decir, $7.5$ minutos en inflar los $50$ globos.

Autoevaluación

Repasemos lo aprendido.

Resuelve los siguientes problemas utilizando la regla de tres directa.