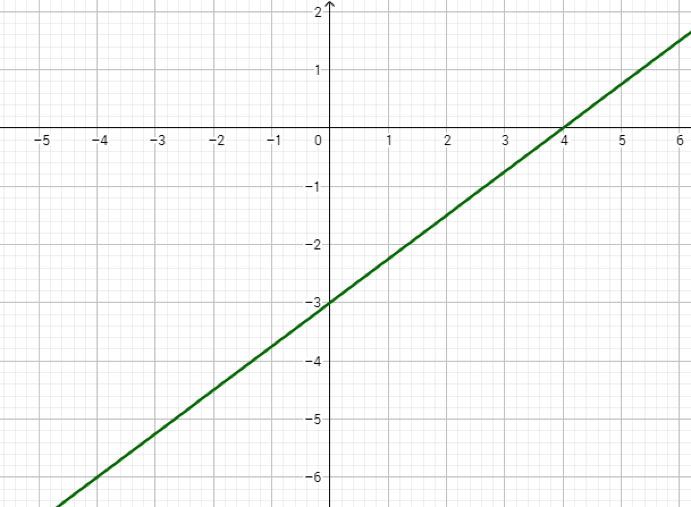
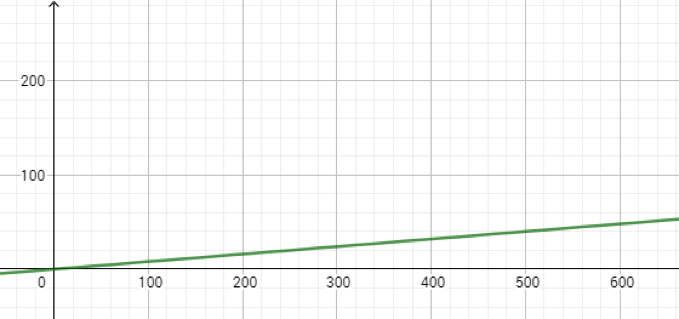
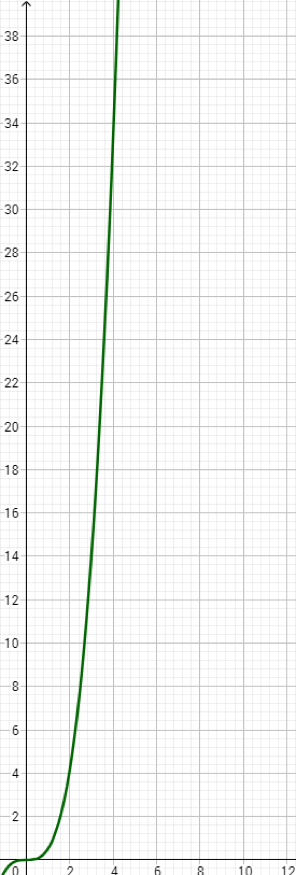
Una función es la relación entre dos o más variables. Por ejemplo, sabemos que la estatura de una persona es función de su edad y decimos que la estatura está en función de la edad en años. Aquí las variablesestatura y edad, están relacionadas de modo que la estatura depende de la edad. Entonces, en este ejemplo, la edad es una variable independiente y la estatura es una variable dependiente.

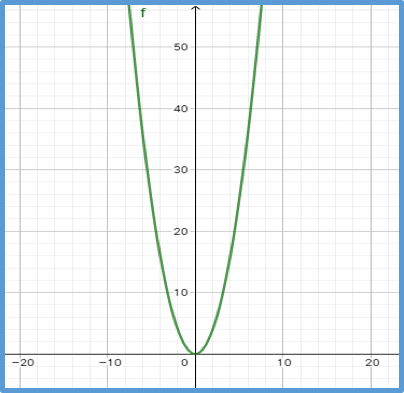
Es muy útil pensar en una función $f$ como una máquina en la que “la entrada” es $x$ elemento del dominio y “la salida” es $f(x)$ elemento de su codominio.

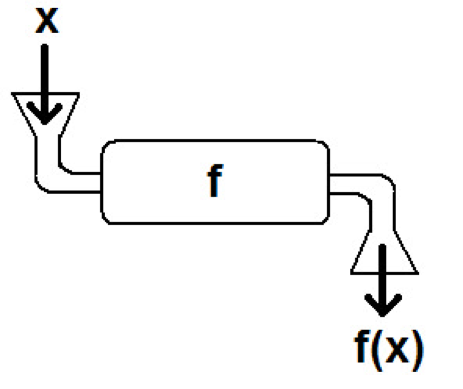
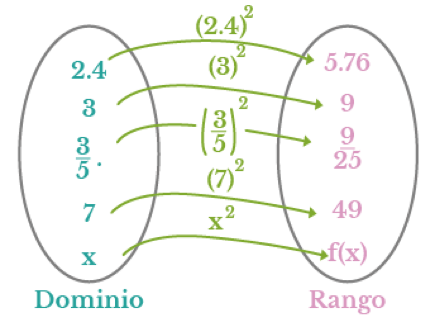
También es muy cómodo ilustrar una función mediante un diagrama de flechas en el que cada flecha indica específicamente qué elemento del dominio se relaciona con qué elemento del codominio.

Otras formas de representar funciones que nos ayudan a entenderlas mejor, son las siguientes:

• VERBAL: Usando una descripción con palabras. Por ejemplo: la función que a cada persona le asigna la primera letra de su apellido paterno, o la que a cada automóvil le asigna un número de placa.
• ALGEBRAICA: Mediante una fórmula o expresión algebraica que exhiba explícitamente la regla de correspondencia que determina el valor de $f(x)$ para cada $x$ del dominio de $f$. Ejemplo: $$f(x)=x^{2}$$
• NUMÉRICA: Usando una tabla de valores en la que se describen en una columna los elementos del dominio y en la otra los del codominio. Dos elementos estarán en el mismo renglón cuando estén relacionados. Ejemplo:

  Dominio	Codominio
  $x$	$f(x)$
  -1	1
  0	0
  $\frac{3}{5}$	$\frac{9}{25}$
  $\frac{1}{3}$	$\frac{1}{9}$

  Aquí la función es: $f(x)=x^{2}$

• GRÁFICA: Mediante un dibujo llamado gráfica de la función y que es su representación en el plano cartesiano. Si tenemos la función $f:A \rightarrow B$ su gráfica es la colección de puntos $$\{(x,f(x))| x \in A\}$$ Ejemplo:


Gráfica de la función $f(x)=x^{2}$

Ejemplo

Representemos de las cuatro formas descritas, una función que transforme la temperatura Fahrenheit en Celsius.

• Representación verbal. Para convertir de Celsius a Fahrenheit , multiplicar la temperatura Celsius por $\frac{9}{5}$ y luego sumar 32.
• Representación algebraica. Siguiendo la descripción verbal, pondremos como variable independiente la temperatura dada en Celsius, representada con la letra $C$, y $F(C)$ será la temperatura Fahrenheit. Así, tendremos que: $$F(C)= \frac{9}{5}C+32$$
• Representación numérica. Con la descripción algebraica, es muy fácil obtener una tabla de valores:

C	F(C)
-10	14
0	32
10	50
20	68
30	86
40	104

• Representación gráfica. Mediante los puntos tabulados en la representación anterior, es muy sencillo obtener la gráfica:

Autoevaluación

Para las siguientes funciones descritas verbalmente encuentra sus representaciones algebraica, numérica y gráfica.

1. La función $f(x)$ se obtiene dividiendo la entrada entre 3 y luego, sumando $\frac{2}{3}$ al resultado.

2. La función $g(x)$ se obtiene restando 4 a la entrada y multiplicando el resultado por $\frac{3}{4}$.

3. Sea $T(x)$ el impuesto cobrado a una mueblería por $x$ pesos de ventas. Para encontrar el impuesto hay que calcular el $8\%$.

4. Sea $V(d)$ el volumen de una esfera de diámetro $d$. Para calcular el volumen, se toma el cubo del diámetro, se multiplica por $\pi$ y se divide por 6.