¿Qué es el tiro vertical?

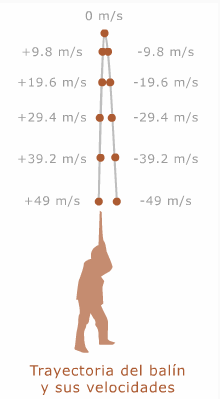
Un tiro vertical (por ejemplo, lanzar hacia arriba una pelota) se puede ver como la unión de dos movimientos de tipo movimiento uniformemente acelerado, (MUA), uno de subida y el otro de bajada. En el de subida, el objeto tiene rapidez inicial hacia arriba e irá disminuyendo la magnitud de su rapidez hasta hacerse cero. En el de bajada, el objeto tiene rapidez inicial 0 m/s e irá aumentando la magnitud de su rapidez (dirigida hacia abajo). En el momento en que regrese al punto de partida, el objeto tendrá rapidez igual en magnitud, pero en sentido contrario a la que tenía inicialmente.

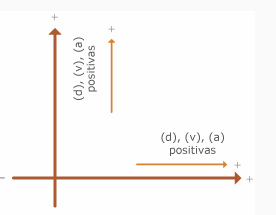
Por lo anterior se hace necesaria una designación, totalmente convencional, del signo de las direcciones, de modo que adoptaremos la tradicional relación de signos: positivo (+) al desplazamiento, velocidad y aceleración dirigidas hacia arriba o a la derecha, y negativo (-) al desplazamiento, velocidad y aceleración dirigidas hacia abajo o a la izquierda. Observa en la siguiente gráfica que lo conveniente de esta asignación es que coincide con los signos de los ejes coordenados en el plano cartesiano:

Clic para ver más grande

De acuerdo a la convención de signos que acabamos de consentir, tendremos que en un tiro vertical:

• El desplazamiento es positivo en la primera parte y negativo en la segunda.
• La velocidad inicial del objeto es positiva, pero va disminuyendo y en determinado momento será igual a cero, después llegará a un valor igual en magnitud pero de sentido (signo) contrario.
• La aceleración de la gravedad (g=- 9.8 m/s²) siempre será negativa dado que siempre está dirigida hacia abajo.

Ahora que aceptamos la convención, podemos ir al tiro vertical.

Preguntémonos, ¿cómo es el movimiento de los objetos al subir? A continuación, a partir de su comportamiento te darás cuenta de que, en muchos sentidos, es parecido al descenso.

Piensa en el siguiente caso hipotético: Un joven tiene un rifle de municiones que apunta verticalmente hacia arriba y después dispara una munición (pequeño balín). Al momento de salir disparado, el balín tiene una velocidad igual a 49 m/s (que equivale a 176 km/hr). Dado que el disparo es vertical hacia arriba, entonces el balín tendrá una trayectoria de subida y bajada por un solo camino, en determinado momento llegará a una altura máxima y después empezará a descender. Es precisamente en ese punto de máxima altura que el balín tendrá, por un instante, velocidad igual a 0 m/s. Después de alcanzar la máxima altura en su trayectoria, el balín desciende, comenzando con una velocidad igual a 0 m/s y posteriormente esta velocidad se incrementará, pero en sentido negativo (hacia abajo).

Clic para ver más grande

Como estamos haciendo la suposición de que no hay fricción con el aire, entonces encontraremos que la velocidad con la que inició su movimiento será la misma en magnitud (pero de signo contrario) que la que tiene cuando regresa al punto de partida. Esto es, que el movimiento de bajada es una “imagen de espejo” del movimiento de subida.

¿Por qué crees que el ascenso y descenso se muestran como movimientos similares en sus características? Piensa un poco en tu respuesta.

El ascenso y descenso libres de un objeto tienen características similares debido a que los dos son movimientos regidos por una única fuerza (gravitacional). Se mueven sobre una línea vertical y la velocidad es 0 m/s en uno de los extremos de sus trayectorias.

Partiendo de nuestra suposición inicial, el balín es disparado verticalmente hacia arriba y tiene una velocidad inicial de 49 m/s. Dado que está siendo frenado a razón de 9.8 m/s² por una fuerza dirigida hacia abajo, la velocidad irá reduciéndose en 9.8 m/s por cada segundo que transcurra, por lo que demorará 5 segundos en llegar a ser 0 m/s su velocidad (es decir, se detendrá), como se muestra en la siguiente tabla:

Dicho de otra manera, le llevará 5 segundos al balín llegar a lo más alto de su trayectoria. Pero como la fuerza de gravedad siempre actúa sobre el balín, éste seguirá acelerándose negativamente (es decir, hacia abajo), lo cual provocará que ahora el balín empiece su descenso y siga incrementando negativamente su velocidad, por lo que al tiempo t = 6 s, la velocidad del balín será –9.8 m/s, y al siguiente segundo será –19.6 m/s.

Observa la tabla con algunos valores de la velocidad del balín en toda su trayectoria

¿Quieres visualizar la trayectoria del balín? Recuerda que las trayectorias de subida y la de bajada pasan por los mismos puntos, sólo que en este dibujo se colocaron separadas para no confundirlas. También puedes observar que, en determinado punto, la velocidad de subida es la misma en magnitud, pero de signo contrario que la velocidad de bajada. Por ejemplo, en el punto de partida, tiene velocidad 49 m/s y en el punto de llegada (que es el mismo del que partió el balín) tiene velocidad –49 m/s. Lo anterior también es válido para cualquier punto de la trayectoria, es decir, si en cierto punto la velocidad en la subida del balín es +35.7 m/s, entonces la velocidad del balín en la bajada será -35.7 m/s.

Clic para ver más grande

Sin embargo, no basta verlo en el dibujo por lo que vamos a verificarlo con las siguientes ecuaciones.

En el caso del MUA, la fórmula para calcular la aceleración es:

Donde $V_f$ es la velocidad final, $V_0$ la velocidad inicial y $t$ representa al tiempo de recorrido. En el caso del balín disparado por el rifle tendrá velocidad inicial $V_0 = 49 \:m/s$ y sabemos que la aceleración es $a=g=-9.8m/s^2$. de modo que para averiguar la velocidad final se despeja de la ecuación anterior y obtenemos que:

$V_f = at + V_0$

por lo que en el tiempo $t = 1\:s$, tendremos:

$V_f = (-9.8 m/s^2)(1s) + 49 m/s = -9.8 m/s + 49 m/s = 39.2 m/s$

y de manera similar podemos obtener la velocidad del balín para $t = 9\:s:$

$V_f = (-9.8 \frac{m}{s^2})(9s) + 49\frac{m}{s} = -88.2\frac{m}{s} + 49\frac{m}{s} = 39.2m/s$

Empleando este mismo procedimiento puedes comprobar los valores de la tabla para la velocidad del balín. Te invitamos a ejercitarte hallando la velocidad para otros puntos de la trayectoria. Seguramente ya estás convencido que la velocidad del balín en determinado punto de su ascenso es la misma en magnitud, pero de signo contrario que la de su descenso.

Veamos un ejemplo.

Para encontrar la posición del balín podemos usar la ecuación general para analizar el MUA, es decir:

$d = d_0 + V_0t + \frac{at^2}{2}$

Como en este caso nuestro experimento inicia en el momento de ser disparado el balín por el rifle, entonces la posición del balín en el tiempo $t=0\:s$ es precisamente $d_0= 0\:m.$ Por otra parte, la velocidad inicial del balín es $V_0 = 49\: m/s$ y, su aceleración es $a = -9.8\:m/s^2$ (precisamente el valor de $g$). Por ello, al sustituir estos valores en la ecuación, obtenemos que:

$d = 0 + 49t - \frac{9.8t^2}{2}$

o lo que es lo mismo:

$d = 49t - 4.9t^2$

Con ella podemos llenar la siguiente tabla de valores de la posición del balín en los primeros 10 segundos.

De los dos resultados anteriores puedes observar que la posición del balín a los 2.5 s de haber iniciado su movimiento es igual a la posición al momento en que le faltan 2.5 s para terminar su recorrido. Puedes darte cuenta que la máxima altura que alcanza el balín es 122.5 m, y recuerda que este dato fue encontrado con la ayuda de la ecuación:

$d = d_0 + V_0t + \frac{at^2}{2}$

Podemos corroborar este resultado con otra de las ecuaciones del MUA:

$2ad = V^2_f - V^2_0$

al despejar la posición (o distancia), obtenemos:

$d = \frac{V^2_f - V^2_0}{2a}$

Aquí podemos aprovechar el hecho de que, en el punto de máxima altura alcanzada, el móvil tiene velocidad ($V_f$) igual a cero, por lo que la ecuación queda como sigue:

Como ves coincide con el resultado anteriormente obtenido; de modo que podemos estar ciertos de nuestros resultados.

¿Cuál sería la máxima altura alcanzada por el balín si su velocidad inicial fuera solamente de 24.5 m/s (es decir, la mitad de la del ejemplo anterior)?, calculemos

$d = \frac{0^2 - (24.5)^2}{2(-9.8)} = \frac{-600.25}{-19.6} = 30.625$

Como verás, con las poderosas ecuaciones podemos encontrar la velocidad, el tiempo y la distancia recorrida por cualquier objeto que forme parte de un tiro vertical.

Esperamos lo aprendido te sea tan interesante como a nosotros.

Para verificar tus aprendizajes te invitamos resolver la siguiente actividad.

Autoevaluación

En Atlixco, un pueblo mágico del Estado de Puebla, se realiza una feria anual. Uno de los juegos es disparar un proyectil lanzado verticalmente hacia arriba. Quien logre que el proyectil tenga la altura máxima es el ganador de la prueba.

Miguel participa como todos los años en el juego. Lanza su proyectil con una velocidad inicial de 25 m/s. Ayúdale a encontrar sus marcas, respondiendo las siguientes preguntas: