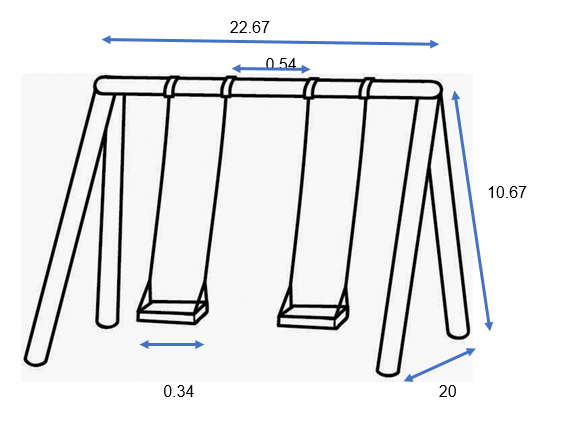
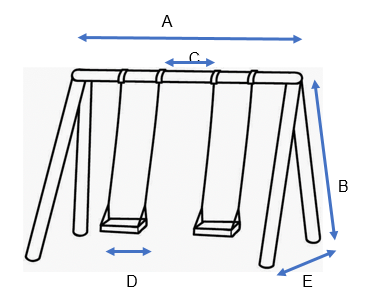
Cuando hablamos de la clasificación de los triángulos de acuerdo a la medida de sus ángulos, se dice que un triángulo rectángulo tiene un ángulo recto, es decir, de 90°. Los lados que forman el ángulo de 90° son llamados catetos y el lado del triángulo opuesto al ángulo recto se llama hipotenusa. Por ejemplo, la figura que se forma al colocar una escalera sobre una pared.

La parte de la escalera desde el piso hasta el contacto con la pared, sería la hipotenusa, la distancia de la pared hasta la base de la escalera es un cateto, la longitud de la pared desde el piso hasta el contacto entre la escalera y la pared también es llamado cateto.
Hablemos del Teorema de Pitágoras. Este teorema dice que la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa.
Podemos expresar el Teorema de Pitágoras como:
$h^2 = c_1^2+c_2^2$
Los datos que conocemos son los catetos, y lo que necesitamos conocer es la longitud de la escalera que sería la hipotenusa. Sólo tienes que sustituir los valores en la fórmula.
.png)
Si tienes un valor elevado al cuadrado y le aplicas raíz cuadrada a ese valor, obtendrás el valor. Siempre que aplicamos una operación a una expresión algebraica, lo debemos hacer en ambos lados de la expresión para mantener el equilibrio de la expresión. Si aplicamos estos conocimientos encontramos el valor de h:
$\sqrt{h^2}=\sqrt{c_1^2+c_2^2}$
$h=\sqrt{c_1^2+c_2^2}$
Regresando al ejemplo de la escalera. Si sabemos que la base de la escalera se encuentra a 2 metros de la pared y la pared tiene una altura de 5 metros, encuentra la longitud de la escalera desde la base hasta el contacto con la pared. (Si el resultado es con decimales, escribe sólo las dos primeras cifras).
Longitud de la escalera: m
done Revisar
Ángulos interiores y exteriores
Fíjate en el Teorema de Pitágoras. Los valores de los lados del triángulo están elevados al cuadrado, esto significa que lo podemos relacionar con áreas, de manera que si construimos cuadrados sobre cada uno de los lados del triángulo, obtenemos la siguiente figura.
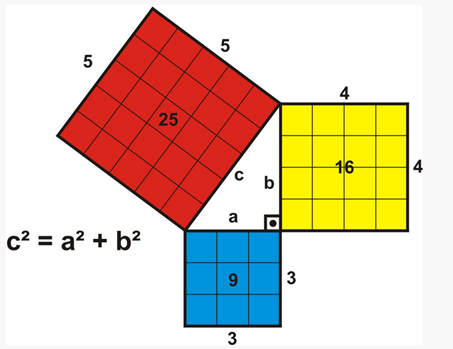
Observa que el cuadrado que se construyó sobre la hipotenusa es el cuadrado con mayor área. Esto es porque de los 3 lados de un triángulo rectángulo, la hipotenusa siempre es el lado más largo.
Además, el teorema dice que la suma de las áreas de los cuadrados que se construyeron sobre los catetos es igual al área que se construyó sobre la hipotenusa.
Para observar el Teorema de Pitágoras de forma geométrica utilizaremos un ejemplo clásico, en el cual los catetos miden 3 y 4 respectivamente. De manera que analíticamente tenemos lo siguiente:
$h=\sqrt{c_1^2+c_2^2}$
$h=\sqrt{3^2+4^2}$
$h=\sqrt{9+16}$
$h=\sqrt{25}$
$h=\frac{+}{-}5$