A continuación, te vamos a mostrar algunas imágenes de zonas arqueológicas que se encuentran en México. Estos tesoros representan uno de los muchos atractivos turísticos de nuestro país.
Palenque se encuentra situado en el borde del este del Río Usumacinta en las colinas de la Sierra Madre Oriental, 130 kilómetros al sur del Golfo de México. Palenque representa la variante regional occidental de la civilización clásica Maya. Ante la necesidad de medir el tiempo, las antiguas civilizaciones se guiaban por el día y la noche o los ciclos de la luna.

La ciudad de Teotihuacán, también conocida como La ciudad de los Dioses, data del año 200 a.C. y sobrevivió hasta alrededor de los años 750 d.C. Contaba con unos $20 km^2$ y aproximadamente 150 mil habitantes en su época de florecimiento. Se encuentra ubicada a unos 50 km al norte de lo que hoy conocemos como la Ciudad de México.

Chichén Itzá es una ciudad arqueológica maya del estado mexicano de Yucatán. El nombre de Chichén-Itzá tiene raíz maya y significa "en la orilla del pozo de los itzáes". Se estima que Chichén-Itzá fue construida alrededor de los años 435 y 455 de nuestra era.

Las construcciones son impresionantes, pero ¿te imaginas la cantidad de trabajo que hay detrás de estas construcciones? Más aún si pensamos que en el tiempo en que fueron hechas no contaban con las herramientas que tenemos actualmente. Estas construcciones tienen características similares. Asombrosamente, las construcciones tienen formas geométricas casi perfectas, y para nosotros es un verdadero misterio de cómo es que se llevaron a cabo tales obras de arte. Como te podrás dar cuenta, los arquitectos antiguos tenían una visión espacial impresionante: algunas figuras que nosotros alcanzamos a diferenciar son triángulos, rectángulos, trapecios y cuadrados. Observa con cuidado las imágenes y dinos si identificas alguna figura más…
Después de tus observaciones, te sugerimos que te fijes en las cosas que te rodean e identifiques figuras geométricas.
Me imagino que encontraste una gran cantidad de objetos con formas geométricas. La Geometría es muy importante; justamente una de sus aplicaciones es el diseño de objetos. Por eso es interesante conocer las características de algunas figuras geométricas. Por ejemplo, un triángulo es una figura plana que tiene 3 lados, 3 vértices que son la intersección de sus lados y 3 ángulos que son la abertura entre sus lados.
Veamos el triángulo con más detalle.
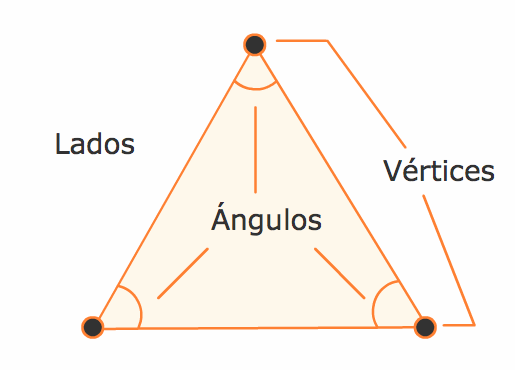
De acuerdo a los componentes de un triángulo, se pueden clasificar de dos maneras:
Por la longitud de sus lados
Triángulo escaleno
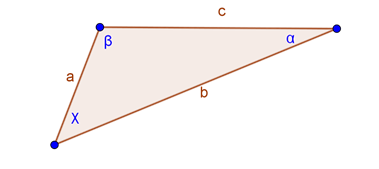
Este triángulo tiene sus lados y ángulos diferentes.
Triángulo equilátero

Es un triángulo particular, ya que sus ángulos siempre miden 60° y sus 3 lados miden lo mismo.
Triángulo isósceles
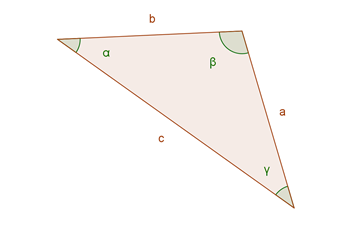
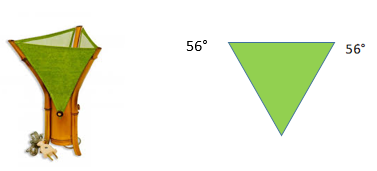
Este triángulo tiene dos lados iguales, y dos ángulos iguales. Observa la figura del triángulo isósceles. Los ángulo iguales también son iguales.
Por la medida de sus ángulos
Triángulo rectángulo
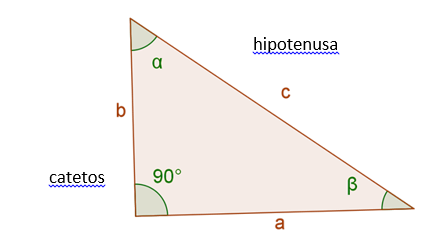
Este triángulo tiene un ángulo recto, o sea, un ángulo de 90°. Los lados que forman el ángulo recto, se llaman catetos. El lado opuesto al ángulo recto es conocido como hipotenusa. Generalmente el ángulo de $90°$ se señala con una marca en escuadra como se observa en la figura.
Triángulos acutángulos

Tienen sus tres ángulos agudos (miden menos de 90°).
Triángulos obtusángulo
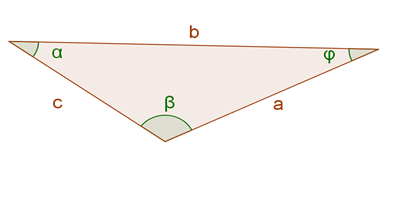
Este triángulo tiene un ángulo obtuso. Un ángulo obtuso es mayor a 90°.
Rectas notables en el triángulo
Existe 4 rectas importantes que son trascendentales en las construcciones del triángulo.
1. Mediana
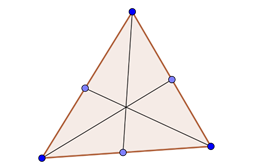
Es el segmento trazado desde un vértice hasta el punto medio del lado opuesto. La intersección de las medianas se llama “Baricentro”. El baricentro es el centro de gravedad del triángulo, o sea, el punto donde se encuentra el peso total del triángulo.
2. Altura

Es la perpendicular a un lado, que pasa por el vértice opuesto. El punto donde se intersectan las 3 alturas se llama “Ortocentro”.
3. Bisectriz
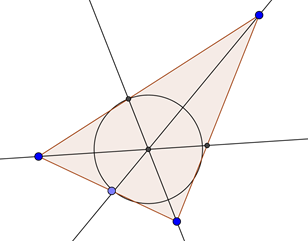
Es la recta que divide a un ángulo en dos ángulos iguales. El punto de intersección de las 3 bisectrices se llama “Incentro”. Se llama incentro porque constituye el centro de una circunferencia que se encuentra dentro del triángulo.
4. Mediatriz

Es la perpendicular en el punto medio de cada lado del triángulo. El punto de intersección entre las mediatrices se llama “Circuncentro”. Se llama circuncentro porque la intersección de las mediatrices es el centro de la circunferencia que pasa por los 3 vértices del triángulo. Es decir, el triángulo está dentro de la circunferencia.