Introducción

¿Cómo podemos saber si dos variables están relacionadas por una variación lineal?.

Si $y$ es la variable dependiente y $x$ la variable independiente, ambas están relacionadas por una variación lineal si se cumple que $y=mx+b$. En esta expresión $m$, representa la constante de variación lineal, o constante de proporcionalidad.

Si graficamos en el plano todos los puntos $(x,mx+b)$ que cumplen la relación, esta gráfica es una recta que no pasa por el origen, el punto $(0, 0)$ sino por el punto $(0,b) \: b \neq 0.$

Es decir, la gráfica sería una recta de ordenada al origen $b \neq 0$ y pendiente $m$: la constante que indica el valor de la variación lineal.

Esta constante se calcula como $m=\frac{y_2-y_1}{x_2-x_1}$

Donde ($x_1,y_1$) y ($x_2,y_2$) son dos parejas de valores que satisfacen la relación que analizamos.

Gráfica de una relación que representa una variación lineal

Como dijimos, la gráfica que representa una variación lineal es una línea recta que pasa por el punto $(0 , b).$

La siguiente tabla representa observaciones de velocidad y tiempo.

Con los datos dados, encuentra lo siguiente:

1. La ecuación que representa la recta
2. La constante de variación lineal $m$ y la ordenada al origen $b$
3. Realiza la gráfica

Primeramente, expresemos los datos en la tabla como dos variables que están relacionadas. Hay que determinar cuál es la variable dependiente y cuál la independiente.

En este caso, sabemos que la velocidad depende del tiempo. Es decir, $v$ es la variable dependiente y $t$ la independiente.

Para obtener la constante de variación lineal recuerda la expresión que define a la pendiente. En este ejemplo, si tenemos dos pares de los valores dados en la tabla, $(t_1,v_1)$, $(t_2,v_2)$, entonces, $m$ quedará definida como $$m=\frac{v_2-v_1}{t_2-t_1}$$

Sustituyamos para obtener la constante de variación:

$m=\frac{3\frac{m}{s}-1\frac{m}{s}}{1s-0s}=\frac{2\frac{m}{s}}{1s}=2\frac{m}{s^2}$

$m=\frac{5\frac{m}{s}-3\frac{m}{s}}{2s-1s}=\frac{2\frac{m}{s}}{1s}=2\frac{m}{s^2}$

$m=\frac{7\frac{m}{s}-5\frac{m}{s}}{3s-2s}=\frac{2\frac{m}{s}}{1s}=2\frac{m}{s^2}$

Vemos que, en efecto, las variables están relacionadas mediante variación lineal pues $m$, la pendiente, es constante $m=2\frac{m}{s^2}$. Esta es la constante de variación lineal de esta relación.

Para obtener $b$, debemos observar cuál es el valor que se obtiene cuando la variable independiente es cero, eso sucede cuando $v= 1\: m/s$, por lo que la ecuación que representa la relación entre estas dos variables es $v=2t+1$.

La gráfica, sabemos que es una recta:

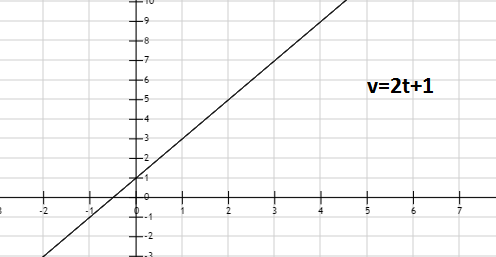
Observa que para verificar si las variables $v$ y $t$ están relacionadas por una variación lineal, lo que hicimos fue calcular la variación de cada variable (la diferencia entre dos valores de $t$ y la diferencia entre dos valores de $v$) y luego obtuvimos el cociente de la variación de la variable independiente entre la variación de la variable dependiente. Como el resultado de este cociente es una constante, concluimos que en efecto, $v$ y $t$ están relacionadas por una variación lineal.

Frecuentemente la variación de una variable $x$, se llama también la incremento en $x$ y se denota como $\Delta x$.

Hagamos un ejercicio más

Suponiendo que en los datos de la siguiente tabla, $y$ es la variable independiente y $x$ la dependiente, identifica si la relación entre ellas presenta variación lineal.

Tomemos dos pares de datos dados en la tabla. Digamos $x=0, y= 3$ y $x=1, y=9$.

¿Cuál es la variación de $y$? $$\Delta y=9 – 3 =6$$

¿Cuál es la variación de $x$? $$\Delta x= 1 – 0 =1$$

Entonces, el cociente de la variación de la variable independiente entre la variación de la variable dependiente es $\frac{\Delta y}{\Delta x} = \frac{6}{1}=6$

Tomemos otras dos parejas de datos $x= 2, y= 15$ y $x=5, y=33$.

Entonces, ahora tenemos que: $\frac{\Delta y}{\Delta x} = \frac{33-15}{5-2}=\frac{18}{3}=6$

Es decir, la variación es constante (compruébalo intentando con otras dos parejas de datos) la constante de proporcionalidad es $6$, y cuando $x=0$, el valor de $y$ es $3$, por lo que la expresión algebraica que describe esta relación es $y=6x+3.$

Un último ejercicio

Supongamos que los datos dados en la siguiente tabla se relacionan con variación lineal. Comprueba esta afirmación y llena los espacios en blanco para completarla.

Tomemos dos parejas de valores de la tabla $(2,0)$ y $(3,-2).$

$$\frac{\Delta y}{\Delta x} = \frac{-2-0}{3-2}=\frac{-2}{1}=-2$$

Elijamos otras dos parejas. Observa que puedes elegir los que quieras, $(4,-4)$ y $(10,-16)$

$$\frac{\Delta y}{\Delta x} = \frac 10-4=\frac{-16+4}{6}=\frac{-12}{6}=-2$$

Entonces, en efecto estos datos presentan variación lineal y la pendiente o constante de variación lineal es $m=-2$.

Ahora completemos la tabla.

Para $x=1$, llamemos $y_2$ a su correspondiente valor en $y$. Junto con el par $(3,-2)$ calculemos la variación lineal (que ya sabemos, es $-2$.)

$$\frac{\Delta y}{\Delta x} = \frac{y_2-(-2)}{1-3}=\frac{y_2+2}{-2}=-2$$

Tenemos que $$\frac{y_2+2}{-2}=-2$$

$$\Rightarrow y_2+2=(-2)(-2)=4$$

$$\therefore y_2=2$$

Por lo que la pareja que falta es $(1,2)$.

Haciendo lo mismo ahora para $x=0$ y la pareja $(4,-4)$, tenemos:

$$\frac{\Delta y}{\Delta x} = \frac{y_2-(-4)}{0-4}=\frac{y_2+4}{-4}=-2$$

$$\Rightarrow y_2+4 =8 \: \therefore y_2=4$$

Así, la última la pareja faltante es $(0,4)$. La tabla queda de la manera siguiente:

Sabemos que el valor de $b$ se obtiene cuando $x=0$, por lo que en este caso es $b=4$, la expresión algebraica que define esta relación es $y=-2x+4.$

Autoevaluación

1. Verifica si los siguientes datos presentan variación lineal y obtén, si es el caso, la expresión algebraica y su gráfica. Completa la tabla.

   $x$	0	4	5	6	7	10
   $y$		18	27	36	45	72

2. De acuerdo a la expresión $y=2x+2.5$, llena la tabla siguiente y obtén su gráfica.

   $x$	-1	0	2	(b)	5	7
   $y$	0.5	(a)	6.5	10.5	(c)	16.5

Verifica tus respuestas aquí class